
Legendre's equation
Encyclopedia
In mathematics, Legendre's equation is the Diophantine equation
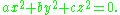
The equation is named for Adrien Marie Legendre who proved in 1785 that it is solvable in integers x, y, z, not all zero, if and only if
−bc, −ca and −ab are quadratic residues modulo a, b and c, respectively, where a, b, c are nonzero, square-free
, pairwise relatively prime integers
, not all positive or all negative .
Diophantine equation
In mathematics, a Diophantine equation is an indeterminate polynomial equation that allows the variables to be integers only. Diophantine problems have fewer equations than unknown variables and involve finding integers that work correctly for all equations...
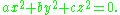
The equation is named for Adrien Marie Legendre who proved in 1785 that it is solvable in integers x, y, z, not all zero, if and only if
−bc, −ca and −ab are quadratic residues modulo a, b and c, respectively, where a, b, c are nonzero, square-free
Square-free integer
In mathematics, a square-free, or quadratfrei, integer is one divisible by no perfect square, except 1. For example, 10 is square-free but 18 is not, as it is divisible by 9 = 32...
, pairwise relatively prime integers
Pairwise coprime
In mathematics, especially number theory, a set of integers is said to be pairwise coprime if every pair of distinct integers a and b in the set are coprime...
, not all positive or all negative .

