Lawson criterion
Encyclopedia
In nuclear fusion
research, the Lawson criterion, first derived on fusion reactors (initially classified) by John D. Lawson
in 1955 and published in 1957, is an important general measure of a system that defines the conditions needed for a fusion reactor to reach ignition, that is, that the heating of the plasma by the products of the fusion reactions is sufficient to maintain the temperature of the plasma against all losses without external power input. As originally formulated the Lawson criterion gives a minimum required value for the product of the plasma (electron) density ne and the "energy confinement time" τE. Later analyses suggested that a more useful figure of merit
is the "triple product" of density, confinement time, and plasma temperature T. The triple product also has a minimum required value, and the name "Lawson criterion" often refers to this inequality.
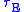measures the rate at which a system loses energy to its environment. It is the energy content W divided by the power loss 
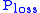(rate of energy loss):
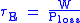
For a fusion reactor to operate in steady state, as magnetic fusion energy schemes usually entail, the fusion plasma must be maintained at a constant temperature. Thermal energy must therefore be added to it (either directly by the fusion products or by recirculating some of the electricity generated by the reactor) at the same rate the plasma loses energy (for instance by heat conduction to the device walls or radiation losses like bremsstrahlung
).
For illustration, the Lawson criterion for the D-T reaction will be derived here, but the same principle can be applied to other fusion fuels. It will also be assumed that all species have the same temperature, that there are no ions present other than fuel ions (no impurities and no helium ash), and that D and T are present in the optimal 50-50 mixture. In that case, the ion density is equal to the electron density and the energy density of both together is given by
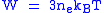
where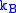
is the Boltzmann constant.
The volume rate f (reactions per volume per time) of fusion reactions is
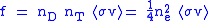
where σ is the fusion cross section
, v is the relative velocity, and < > denotes an average over the Maxwellian velocity distribution at the temperature T.
The volume rate of heating by fusion is f times Ech, the energy of the charged fusion products (the neutrons cannot help to keep the plasma hot). In the case of the D-T reaction, Ech = 3.5 MeV.
The Lawson criterion is the requirement that the fusion heating exceed the losses:
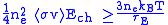
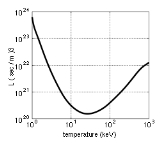
The quantity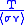
is a function of temperature with an absolute minimum. Replacing the function with its minimum value provides an absolute lower limit for the product 
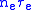. This is the Lawson criterion.
For the D-T reaction, the physical value is at least
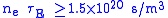
The minimum of the product occurs near T = 25 keV
.
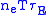. For most confinement concepts, whether inertial
, mirror
, or toroidal confinement, the density and temperature can be varied over a fairly wide range, but the maximum pressure attainable is a constant. When that is the case, the fusion power density is proportional to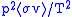
. Therefore the maximum fusion power available from a given machine is obtained at the temperature where 
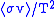is a maximum. Following the derivation above, it is easy to show the inequality
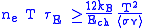
For the special case of tokamak
s there is an additional motivation for using the triple product. Empirically, the energy confinement time is found to be nearly proportional to n1/3/P2/3. In an ignited plasma near the optimum temperature, the heating power P is equal to the fusion power and therefore proportional to n2T2. The triple product scales as
Thus the triple product is only a weak function of density and temperature and therefore a good measure of the efficiency of the confinement scheme.
The quantity
is also a function of temperature with an absolute minimum at a slightly lower temperature than 
.
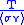For the D-T reaction, the physical value is about
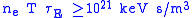
This number has not yet been achieved in any reactor, although the latest generations of machines have come close. For instance, the TFTR has achieved the densities and energy lifetimes needed to achieve Lawson at the temperatures it can create, but it cannot create those temperatures at the same time. ITER
aims to do both.
as well as to magnetic confinement fusion
but is more usefully expressed in a different form. Whereas the energy confinement time in a magnetic system is very difficult to predict or even to establish empirically, in an inertial system it must be on the order of the time it takes sound waves to travel across the plasma:
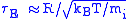
Following the above derivation of the limit on neτE, we see that the product of the density and the radius
must be greater than a value related to the minimum of T3/2/<σv>. This condition is traditionally expressed in terms of the mass density ρ:
To satisfy this criterion at the density of solid D-T (0.2 g/cm³) would require an implausibly large laser pulse energy. Assuming the energy required scales with the mass of the fusion plasma (Elaser ~ ρR3 ~ ρ-2), compressing the fuel to 103 or 104 times solid density would reduce the energy required by a factor of 106 or 108, bringing it into a realistic range. With a compression by 103, the compressed density will be 200 g/cm³, and the compressed radius can be as small as 0.05 mm. The radius of the fuel before compression would be 0.5 mm. The initial pellet will be perhaps twice as large since most of the mass will be ablated
during the compression.
The fusion power density is a good figure of merit to determine the optimum temperature for magnetic confinement, but for inertial confinement the fractional burn-up of the fuel is probably more useful. The burn-up should be proportional to the specific reaction rate (n²<σv>) times the confinement time (which scales as T-1/2) divided by the particle density n:
Thus the optimum temperature for inertial confinement fusion is that which maximizes <σv>/T3/2, which is slightly higher than the optimum temperature for magnetic confinement.
Nuclear fusion
Nuclear fusion is the process by which two or more atomic nuclei join together, or "fuse", to form a single heavier nucleus. This is usually accompanied by the release or absorption of large quantities of energy...
research, the Lawson criterion, first derived on fusion reactors (initially classified) by John D. Lawson
John D. Lawson (scientist)
John David Lawson FRS was a British engineer and physicist.He was born in Coventry and educated at Wolverhampton Grammar School before going on to St John's College, Cambridge, to study for the short Mechanical Sciences degree, including a special wartime radio course...
in 1955 and published in 1957, is an important general measure of a system that defines the conditions needed for a fusion reactor to reach ignition, that is, that the heating of the plasma by the products of the fusion reactions is sufficient to maintain the temperature of the plasma against all losses without external power input. As originally formulated the Lawson criterion gives a minimum required value for the product of the plasma (electron) density ne and the "energy confinement time" τE. Later analyses suggested that a more useful figure of merit
Figure of merit
A figure of merit is a quantity used to characterize the performance of a device, system or method, relative to its alternatives. In engineering, figures of merit are often defined for particular materials or devices in order to determine their relative utility for an application...
is the "triple product" of density, confinement time, and plasma temperature T. The triple product also has a minimum required value, and the name "Lawson criterion" often refers to this inequality.
The product neτE
The confinement time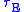 measures the rate at which a system loses energy to its environment. It is the energy content W divided by the power loss (rate of energy loss):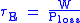For a fusion reactor to operate in steady state, as magnetic fusion energy schemes usually entail, the fusion plasma must be maintained at a constant temperature. Thermal energy must therefore be added to it (either directly by the fusion products or by recirculating some of the electricity generated by the reactor) at the same rate the plasma loses energy (for instance by heat conduction to the device walls or radiation losses like bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
).
For illustration, the Lawson criterion for the D-T reaction will be derived here, but the same principle can be applied to other fusion fuels. It will also be assumed that all species have the same temperature, that there are no ions present other than fuel ions (no impurities and no helium ash), and that D and T are present in the optimal 50-50 mixture. In that case, the ion density is equal to the electron density and the energy density of both together is given by
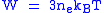
where
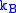is the Boltzmann constant.The volume rate f (reactions per volume per time) of fusion reactions is
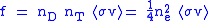
where σ is the fusion cross section
Cross section (physics)
A cross section is the effective area which governs the probability of some scattering or absorption event. Together with particle density and path length, it can be used to predict the total scattering probability via the Beer-Lambert law....
, v is the relative velocity, and < > denotes an average over the Maxwellian velocity distribution at the temperature T.
The volume rate of heating by fusion is f times Ech, the energy of the charged fusion products (the neutrons cannot help to keep the plasma hot). In the case of the D-T reaction, Ech = 3.5 MeV.
The Lawson criterion is the requirement that the fusion heating exceed the losses:
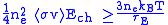
The quantity
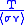is a function of temperature with an absolute minimum. Replacing the function with its minimum value provides an absolute lower limit for the product 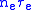. This is the Lawson criterion.For the D-T reaction, the physical value is at least
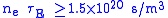
The minimum of the product occurs near T = 25 keV
Electronvolt
In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
.
The "triple product" neTτE
A still more useful figure of merit is the "triple product" of density, temperature, and confinement time,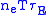. For most confinement concepts, whether inertialInertial confinement fusion
Inertial confinement fusion is a process where nuclear fusion reactions are initiated by heating and compressing a fuel target, typically in the form of a pellet that most often contains a mixture of deuterium and tritium....
, mirror
Magnetic mirror
A magnetic mirror is a magnetic field configuration where the field strength changes when moving along a field line. The mirror effect results in a tendency for charged particles to bounce back from the high field region....
, or toroidal confinement, the density and temperature can be varied over a fairly wide range, but the maximum pressure attainable is a constant. When that is the case, the fusion power density is proportional to
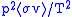. Therefore the maximum fusion power available from a given machine is obtained at the temperature where 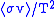is a maximum. Following the derivation above, it is easy to show the inequality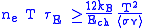For the special case of tokamak
Tokamak
A tokamak is a device using a magnetic field to confine a plasma in the shape of a torus . Achieving a stable plasma equilibrium requires magnetic field lines that move around the torus in a helical shape...
s there is an additional motivation for using the triple product. Empirically, the energy confinement time is found to be nearly proportional to n1/3/P2/3. In an ignited plasma near the optimum temperature, the heating power P is equal to the fusion power and therefore proportional to n2T2. The triple product scales as
- nTτ
nT (n1/3/P2/3) 
nT (n1/3/(n2T2)2/3) 
T -1/3
Thus the triple product is only a weak function of density and temperature and therefore a good measure of the efficiency of the confinement scheme.
The quantity
is also a function of temperature with an absolute minimum at a slightly lower temperature than .For the D-T reaction, the physical value is about
This number has not yet been achieved in any reactor, although the latest generations of machines have come close. For instance, the TFTR has achieved the densities and energy lifetimes needed to achieve Lawson at the temperatures it can create, but it cannot create those temperatures at the same time. ITER
ITER
ITER is an international nuclear fusion research and engineering project, which is currently building the world's largest and most advanced experimental tokamak nuclear fusion reactor at Cadarache in the south of France...
aims to do both.
Inertial confinement
The Lawson criterion applies to inertial confinement fusionInertial confinement fusion
Inertial confinement fusion is a process where nuclear fusion reactions are initiated by heating and compressing a fuel target, typically in the form of a pellet that most often contains a mixture of deuterium and tritium....
as well as to magnetic confinement fusion
Magnetic confinement fusion
Magnetic confinement fusion is an approach to generating fusion power that uses magnetic fields to confine the hot fusion fuel in the form of a plasma. Magnetic confinement is one of two major branches of fusion energy research, the other being inertial confinement fusion. The magnetic approach is...
but is more usefully expressed in a different form. Whereas the energy confinement time in a magnetic system is very difficult to predict or even to establish empirically, in an inertial system it must be on the order of the time it takes sound waves to travel across the plasma:
Following the above derivation of the limit on neτE, we see that the product of the density and the radius
must be greater than a value related to the minimum of T3/2/<σv>. This condition is traditionally expressed in terms of the mass density ρ:- ρR > 1 g/cm²
To satisfy this criterion at the density of solid D-T (0.2 g/cm³) would require an implausibly large laser pulse energy. Assuming the energy required scales with the mass of the fusion plasma (Elaser ~ ρR3 ~ ρ-2), compressing the fuel to 103 or 104 times solid density would reduce the energy required by a factor of 106 or 108, bringing it into a realistic range. With a compression by 103, the compressed density will be 200 g/cm³, and the compressed radius can be as small as 0.05 mm. The radius of the fuel before compression would be 0.5 mm. The initial pellet will be perhaps twice as large since most of the mass will be ablated
Ablation
Ablation is removal of material from the surface of an object by vaporization, chipping, or other erosive processes. This occurs in spaceflight during ascent and atmospheric reentry, glaciology, medicine, and passive fire protection.-Spaceflight:...
during the compression.
The fusion power density is a good figure of merit to determine the optimum temperature for magnetic confinement, but for inertial confinement the fractional burn-up of the fuel is probably more useful. The burn-up should be proportional to the specific reaction rate (n²<σv>) times the confinement time (which scales as T-1/2) divided by the particle density n:
- burn-up fraction ~ n²<σv> T-1/2 / n ~ (nT) (<σv>/T3/2)
Thus the optimum temperature for inertial confinement fusion is that which maximizes <σv>/T3/2, which is slightly higher than the optimum temperature for magnetic confinement.