Language identification in the limit
Encyclopedia
Language identification in the limit is a formal model for inductive inference
. It was introduced by E. Mark Gold in his paper with the same title http://www.isrl.uiuc.edu/~amag/langev/paper/gold67limit.html. In this model, a learner is provided with presentation of some language. The learning is seen as an infinite process. Each time an element of the presentation is read the learner should provide a representation for the language. We say that a learner can identify in the limit a class of languages if given any presentation of any language in the class the learner will produce a finite number of wrong representations, and therefore converge on the correct representation in a finite number of steps, without however necessarily being able to announce its correctness since a counterexample to that representation could appear as an element arbitrarily long after.
Gold defined two types of presentations:
; another learnability model is the so-called Probably approximately correct learning
(PAC) model.
gave the characterizations of learnability from text (positive information) in her paper http://citeseer.ist.psu.edu/context/14508/0.
If a learner is required to be effective, then an indexed class of recursive
languages is learnable in the limit if there is an effective procedure that uniformly enumerates tell-tale
s for each language in the class (Condition 1). It is not hard to see that if we allow an ideal learner (i.e., an arbitrary function), then an indexed class of languages is learnable in the limit if each language in the class has a tell-tale
(Condition 2).
languages has finite thickness, then it is learnable in the limit.
A class with finite thickness certainly satisfies MEF-condition and MFF-condition; in other words, finite thickness implies M-finite thickness.
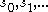and every infinite sequence of languages in the class 
, there exists a finite number n such that 
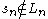implies 
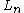is inconsistent with 
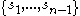. http://www.acm.org/pubs/citations/proceedings/colt/114836/p375-motoki/
It is shown that a class of recursively enumerable languages is learnable in the limit if it has finite elasticity.
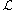if there is an infinite sequence 
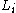of distinct languages in 
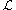and a sequence of finite subset 
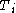such that:
Note that L is not necessarily a member of the class of language.
It is not hard to see that if there is a language with infinite cross property within a class of languages, then that class of languages has infinite elasticity.
Inductive inference
Around 1960, Ray Solomonoff founded the theory of universal inductive inference, the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols...
. It was introduced by E. Mark Gold in his paper with the same title http://www.isrl.uiuc.edu/~amag/langev/paper/gold67limit.html. In this model, a learner is provided with presentation of some language. The learning is seen as an infinite process. Each time an element of the presentation is read the learner should provide a representation for the language. We say that a learner can identify in the limit a class of languages if given any presentation of any language in the class the learner will produce a finite number of wrong representations, and therefore converge on the correct representation in a finite number of steps, without however necessarily being able to announce its correctness since a counterexample to that representation could appear as an element arbitrarily long after.
Gold defined two types of presentations:
- Text (positive information): an enumeration of the language.
- Complete presentation (positive and negative information): an enumeration of all possible strings, each with a label indicating if the string belongs to the language or not.
Learnability
This model is the first known attempt to capture the notion of learnabilityLearnability
-Software testing:In software testing learnability, according to ISO/IEC 9126, is the capability of a software product to enable the user to learn how to use it...
; another learnability model is the so-called Probably approximately correct learning
Probably approximately correct learning
In computational learning theory, probably approximately correct learning is a framework for mathematical analysis of machine learning. It was proposed in 1984 by Leslie Valiant....
(PAC) model.
Learnability characterization
Dana AngluinDana Angluin
-Biography:Professor Angluin is interested in machine learning and computational learning theory. Algorithmic modeling and analysis of learning tasks gives insight into the phenomena of learning, and suggests avenues for the creation of tools to help people learn, and for the design of "smarter"...
gave the characterizations of learnability from text (positive information) in her paper http://citeseer.ist.psu.edu/context/14508/0.
If a learner is required to be effective, then an indexed class of recursive
Recursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
languages is learnable in the limit if there is an effective procedure that uniformly enumerates tell-tale
Tell-tale
A tell-tale or telltale is an indicator, signal, or sign that conveys the status of a situation, mechanism, or system.-Automotive:...
s for each language in the class (Condition 1). It is not hard to see that if we allow an ideal learner (i.e., an arbitrary function), then an indexed class of languages is learnable in the limit if each language in the class has a tell-tale
Tell-tale
A tell-tale or telltale is an indicator, signal, or sign that conveys the status of a situation, mechanism, or system.-Automotive:...
(Condition 2).
Language classes learnable in the limit from text
- Finite cardinality languages
- Pattern languages
Sufficient conditions for learnability
Condition 1 in Angluin's paper is not always easy to verify. Therefore, people come up with various sufficient conditions for the learnability of a language class.Finite thickness
A class of languages has finite thickness if for every string s, there are only a finite number of languages in the class that are consistent with s. This is exactly Condition 3 in Angluin's paper. Angluin showed that if a class of recursiveRecursive
Recursive may refer to:*Recursion, the technique of functions calling themselves*Recursive function, a total computable function*Recursive language, a language which is decidable...
languages has finite thickness, then it is learnable in the limit.
A class with finite thickness certainly satisfies MEF-condition and MFF-condition; in other words, finite thickness implies M-finite thickness.
Finite elasticity
A class of languages is said to have finite elasticity if for every infinite sequence of strings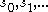 and every infinite sequence of languages in the class , there exists a finite number n such that 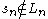implies 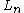is inconsistent with 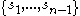. http://www.acm.org/pubs/citations/proceedings/colt/114836/p375-motoki/It is shown that a class of recursively enumerable languages is learnable in the limit if it has finite elasticity.
Infinite cross property
A language L has infinite cross property within a class of languages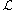 if there is an infinite sequence 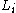of distinct languages in 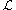and a sequence of finite subset 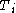such that:
,
,
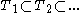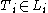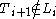, and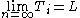
.
Note that L is not necessarily a member of the class of language.
It is not hard to see that if there is a language with infinite cross property within a class of languages, then that class of languages has infinite elasticity.
Relations between concepts
- Finite thickness implies finite elasticity; the converse is not true.
- Finite elasticity and conservatively learnable implies the existence of a mind change bound. http://citeseer.ist.psu.edu/context/1042497/0
- Finite elasticity and M-finite thickness implies the existence of a mind change bound. However, M-finite thickness alone does not imply the existence of a mind change bound; neither does the existence of a mind change bound imply M-finite thickness. http://citeseer.ist.psu.edu/context/1042497/0
- Existence of a mind change bound implies learnability; the converse is not true.
- If we allow for noncomputable learners, then finite elasticity implies the existence of a mind change bound; the converse is not true.
- If there is no accumulation order for a class of languages, then there is a language (not necessarily in the class) that has infinite cross property within the class, which in turn implies infinite elasticity of the class.
Open questions
- If a countable class of recursive languages has a mind change bound for noncomputable learners, does the class also have a mind change bound for computable learners, or is the class unlearnable by a computable learner?