
Landau's constants
Encyclopedia
In complex analysis
, a branch of mathematics, Landau's constants are certain mathematical constant
s that describe the behaviour of holomorphic function
s defined on the unit disk. Consider the set F of all those holomorphic functions f on the unit disk for which
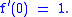
We define Lf to be the radius of the largest disk contained in the image of f, and Bf to be the radius of the largest disk that is the biholomorphic image of a subset of a unit disk.
Landau's constants are then defined as the infimum
of Lf or Bf, where f is any holomorphic function or any injective holomorphic function on the unit disk with
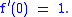
The three resulting constants are abbreviated L, B, and A (for injective functions), respectively.
The exact values of L, B, and A are not known, but it is known that


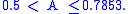
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, a branch of mathematics, Landau's constants are certain mathematical constant
Mathematical constant
A mathematical constant is a special number, usually a real number, that is "significantly interesting in some way". Constants arise in many different areas of mathematics, with constants such as and occurring in such diverse contexts as geometry, number theory and calculus.What it means for a...
s that describe the behaviour of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s defined on the unit disk. Consider the set F of all those holomorphic functions f on the unit disk for which
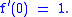
We define Lf to be the radius of the largest disk contained in the image of f, and Bf to be the radius of the largest disk that is the biholomorphic image of a subset of a unit disk.
Landau's constants are then defined as the infimum
Infimum
In mathematics, the infimum of a subset S of some partially ordered set T is the greatest element of T that is less than or equal to all elements of S. Consequently the term greatest lower bound is also commonly used...
of Lf or Bf, where f is any holomorphic function or any injective holomorphic function on the unit disk with
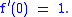
The three resulting constants are abbreviated L, B, and A (for injective functions), respectively.
The exact values of L, B, and A are not known, but it is known that


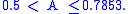
See also
- Table of selected mathematical constants

