Lanchester's laws
Encyclopedia
Lanchester's laws are mathematical formula
e for calculating the relative strengths of a predator/prey pair. This article is concerned with military
forces.
The Lanchester equations are differential equations describing the time dependence of two armies' strengths A and B as a function of time, with the function depending only on A and B.
In 1916, during the height of World War I
, Frederick Lanchester
devised a series of differential equation
s to demonstrate the power relationships between opposing forces. Among these are what is known as Lanchester's Linear Law (for ancient combat
) and Lanchester's Square Law (for modern combat
with long-range weapons such as firearms).
es of men with spear
s, say, one man could only ever fight exactly one other man at a time. If each man kills, and is killed by, exactly one other, then the number of men remaining at the end of the battle is simply the difference between the larger army
and the smaller, assuming identical weapons.
The linear law also applies to unaimed fire into an enemy-occupied area. The rate of attrition depends on the density of the available targets in the target area as well as the number of weapons firing. If two forces, occupying the same land area and using the same weapons, fire randomly into the same target area, they will both suffer the same rate and number of casualties, until the smaller force is eventually eliminated: the greater probability of any one shot hitting the larger force is balanced by the greater number of shots directed at the smaller force.
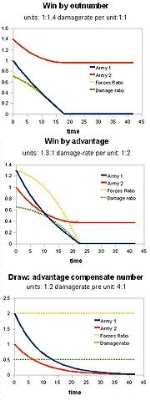
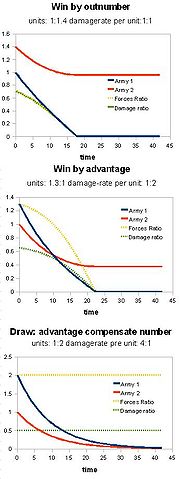 With firearms engaging each other directly with aimed fire from a distance, they can attack multiple targets and can receive fire from multiple directions. The rate of attrition now depends only on the number of weapons firing. Lanchester determined that the power of such a force is proportional not to the number of units it has, but to the square of the number of units. This is known as Lanchester's Square Law.
With firearms engaging each other directly with aimed fire from a distance, they can attack multiple targets and can receive fire from multiple directions. The rate of attrition now depends only on the number of weapons firing. Lanchester determined that the power of such a force is proportional not to the number of units it has, but to the square of the number of units. This is known as Lanchester's Square Law.
More precisely, the law specifies the casualties a firing force will inflict over a period of time, relative to those inflicted by the opposing force. In its basic form, the law is only useful to predict outcomes and casualties by attrition. It does not apply to whole armies, where tactical deployment means not all troops will be engaged all the time. It only works where each man (or ship, unit or whatever) can kill only one equivalent enemy at a time (so it does not apply to machine guns, artillery or—an extreme case—nuclear weapons). The law requires an assumption that casualties build up over time: it does not work in situations in which opposing troops kill each other instantly, either by firing simultaneously or by one side getting off the first shot and inflicting multiple casualties.
Note that Lanchester's Square Law does not apply to technological force, only numerical force; so it takes an N-squared-fold increase in quality to make up for an N-fold increase in quantity.
Let symbol A represent the number of soldiers in the Red force at the beginning of the battle. Each one has offensive firepower α, which is the number of enemy soldiers it can knock out of battle (e.g., kill or incapacitate) per unit time. Likewise, Blue has B soldiers, each with offensive firepower β.
Lanchester’s square law calculates the number of soldiers lost on each side using the following pair of equations . Here, dA/dt represents the rate at which the number of Red soldiers is changing at a particular instant in time. A negative value indicates the loss of soldiers. Similarly, dB/dt represents the rate of change in the number of Blue soldiers.
equations, with two main differences.
First, Lanchester's original equations form a continuous time model, whereas the basic salvo equations form a discrete time model. In a gun battle, bullets or shells are typically fired in large quantities. Each round has a relatively low chance of hitting its target, and does a relatively small amount of damage. Therefore Lanchester’s equations model gunfire as a stream of firepower that continuously weakens the enemy force over time.
By comparison, cruise missiles typically are fired in relatively small quantities. Each one has a high probability of hitting its target, and carries a relatively powerful warhead. Therefore it makes more sense to model them as a discrete pulse (or salvo) of firepower in a discrete time model.
Second, Lanchester's equations include only offensive firepower, whereas the salvo equations also include defensive firepower. Given their small size and large number, it is not practical to intercept bullets and shells in a gun battle. By comparison, cruise missiles can be intercepted (shot down) by surface-to-air missiles and anti-aircraft guns. So it is important to include such active defenses in a missile combat model.
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
e for calculating the relative strengths of a predator/prey pair. This article is concerned with military
Military
A military is an organization authorized by its greater society to use lethal force, usually including use of weapons, in defending its country by combating actual or perceived threats. The military may have additional functions of use to its greater society, such as advancing a political agenda e.g...
forces.
The Lanchester equations are differential equations describing the time dependence of two armies' strengths A and B as a function of time, with the function depending only on A and B.
In 1916, during the height of World War I
World War I
World War I , which was predominantly called the World War or the Great War from its occurrence until 1939, and the First World War or World War I thereafter, was a major war centred in Europe that began on 28 July 1914 and lasted until 11 November 1918...
, Frederick Lanchester
Frederick Lanchester
Frederick William Lanchester, Hon FRAeS was an English polymath and engineer who made important contributions to automotive engineering, aerodynamics and co-invented the field of operations research....
devised a series of differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s to demonstrate the power relationships between opposing forces. Among these are what is known as Lanchester's Linear Law (for ancient combat
Ancient warfare
Ancient warfare is war as conducted from the beginnings of recorded history to the end of the ancient period. In Europe and the Near East, the end of antiquity is often equated with the fall of Rome in 476, and the wars of the Eastern Roman Empire Byzantium in its South Western Asian and North...
) and Lanchester's Square Law (for modern combat
Modern warfare
Modern warfare, although present in every historical period of military history, is generally used to refer to the concepts, methods and technologies that have come into use during and after the Second World War and the Korean War...
with long-range weapons such as firearms).
Lanchester's Linear Law
In ancient combat, between phalanxPhalanx formation
The phalanx is a rectangular mass military formation, usually composed entirely of heavy infantry armed with spears, pikes, sarissas, or similar weapons...
es of men with spear
Spear
A spear is a pole weapon consisting of a shaft, usually of wood, with a pointed head.The head may be simply the sharpened end of the shaft itself, as is the case with bamboo spears, or it may be made of a more durable material fastened to the shaft, such as flint, obsidian, iron, steel or...
s, say, one man could only ever fight exactly one other man at a time. If each man kills, and is killed by, exactly one other, then the number of men remaining at the end of the battle is simply the difference between the larger army
Army
An army An army An army (from Latin arma "arms, weapons" via Old French armée, "armed" (feminine), in the broadest sense, is the land-based military of a nation or state. It may also include other branches of the military such as the air force via means of aviation corps...
and the smaller, assuming identical weapons.
The linear law also applies to unaimed fire into an enemy-occupied area. The rate of attrition depends on the density of the available targets in the target area as well as the number of weapons firing. If two forces, occupying the same land area and using the same weapons, fire randomly into the same target area, they will both suffer the same rate and number of casualties, until the smaller force is eventually eliminated: the greater probability of any one shot hitting the larger force is balanced by the greater number of shots directed at the smaller force.
Description

More precisely, the law specifies the casualties a firing force will inflict over a period of time, relative to those inflicted by the opposing force. In its basic form, the law is only useful to predict outcomes and casualties by attrition. It does not apply to whole armies, where tactical deployment means not all troops will be engaged all the time. It only works where each man (or ship, unit or whatever) can kill only one equivalent enemy at a time (so it does not apply to machine guns, artillery or—an extreme case—nuclear weapons). The law requires an assumption that casualties build up over time: it does not work in situations in which opposing troops kill each other instantly, either by firing simultaneously or by one side getting off the first shot and inflicting multiple casualties.
Note that Lanchester's Square Law does not apply to technological force, only numerical force; so it takes an N-squared-fold increase in quality to make up for an N-fold increase in quantity.
Example Equations
Suppose that two armies, Red and Blue, are engaging each other in combat. Red is firing a continuous stream of bullets at Blue. Meanwhile, Blue is firing a continuous stream of bullets at Red.Let symbol A represent the number of soldiers in the Red force at the beginning of the battle. Each one has offensive firepower α, which is the number of enemy soldiers it can knock out of battle (e.g., kill or incapacitate) per unit time. Likewise, Blue has B soldiers, each with offensive firepower β.
Lanchester’s square law calculates the number of soldiers lost on each side using the following pair of equations . Here, dA/dt represents the rate at which the number of Red soldiers is changing at a particular instant in time. A negative value indicates the loss of soldiers. Similarly, dB/dt represents the rate of change in the number of Blue soldiers.
- dA/dt = -βB
- dB/dt = -αA
Relation to the Salvo Combat Model
Lanchester’s equations are related to the more recent Salvo combat modelSalvo combat model
The salvo combat model provides a mathematical representation of missile battles between modern warships. It was developed by Wayne Hughes at the U.S. Naval Postgraduate School in Monterey . The salvo model describes the basic elements of modern missile combat in a very simple way...
equations, with two main differences.
First, Lanchester's original equations form a continuous time model, whereas the basic salvo equations form a discrete time model. In a gun battle, bullets or shells are typically fired in large quantities. Each round has a relatively low chance of hitting its target, and does a relatively small amount of damage. Therefore Lanchester’s equations model gunfire as a stream of firepower that continuously weakens the enemy force over time.
By comparison, cruise missiles typically are fired in relatively small quantities. Each one has a high probability of hitting its target, and carries a relatively powerful warhead. Therefore it makes more sense to model them as a discrete pulse (or salvo) of firepower in a discrete time model.
Second, Lanchester's equations include only offensive firepower, whereas the salvo equations also include defensive firepower. Given their small size and large number, it is not practical to intercept bullets and shells in a gun battle. By comparison, cruise missiles can be intercepted (shot down) by surface-to-air missiles and anti-aircraft guns. So it is important to include such active defenses in a missile combat model.
Lanchester's Law in use
In modern warfare, to take into account that to some extent both linear and the square apply often an exponent of 1.5 is used.See also
- Attrition warfareAttrition warfareAttrition warfare is a military strategy in which a belligerent side attempts to win a war by wearing down its enemy to the point of collapse through continuous losses in personnel and matériel....
- Maneuver warfareManeuver warfareManeuver warfare, or manoeuvre warfare , is the term used by military theorists for a concept of warfare that advocates attempting to defeat an adversary by incapacitating their decision-making through shock and disruption brought about by movement...
- Lewis Fry RichardsonLewis Fry RichardsonLewis Fry Richardson, FRS was an English mathematician, physicist, meteorologist, psychologist and pacifist who pioneered modern mathematical techniques of weather forecasting, and the application of similar techniques to studying the causes of wars and how to prevent them...
- Salvo combat modelSalvo combat modelThe salvo combat model provides a mathematical representation of missile battles between modern warships. It was developed by Wayne Hughes at the U.S. Naval Postgraduate School in Monterey . The salvo model describes the basic elements of modern missile combat in a very simple way...
External links
- "Kicking Butt By the Numbers: Lanchester's Laws", a Designer's Notebook column by Ernest Adams in the Gamasutra webzine
- Lanchester Equations and Scoring Systems, appendix to "Aggregation, Disaggregation, and the 3:1 Rule in Ground Combat" by Paul K. Davis, Rand Corporation publication MR-638-AF/A/OSD
- Lanchester combat models, "Mathematics Today", 2006, Vol 42/5, pages 170-173.
- lanchester.com
- "Lanchester Laws: In Sales Campaigns" You can find a White Paper here describing the application of Lanchester Theory to High Value Sales Models in the Business World.

