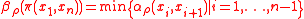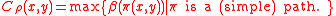Lambda-connectedness
Encyclopedia
In applied mathematics
, lambda-connectedness (or λ-connectedness) deals with partial connectivity for a discrete space
.
Assume that a function on a discrete space (usually a graph
) is given. A degree of connectivity (connectedness) will be defined to measure the connectedness of the space with respect to the function. It was invented to create a new method for image segmentation
. The method has expanded to handle other problems related to uncertainty for incomplete information analysis.
For a digital image and a certain value of , two pixels are called
, two pixels are called  -connected if there is a path linking those two pixels and the connectedness of this path is at least
-connected if there is a path linking those two pixels and the connectedness of this path is at least  .
.  -connectedness is an equivalence relation.
-connectedness is an equivalence relation.
, two points are connected if there is a continuous
function that could move from one point to another continuously. In management science, for example, in an institution,
two individuals are connected if one person is under the supervision of the other. Such connected relations only describe either full connection or no connection. lambda-connectedness is introduced to measure incomplete or fuzzy relations between two vertices, points, human beings, etc.
In fact, partial relations have been studied in other aspects. Random graph
theory allows one to assign a probability
to each edge of a graph. This method assumes, in most cases, each edge has the same probability. On the other hand, Bayesian networks are often used for inference and analysis when relationships between each pair of states/events, denoted by vertices, are known. These relationships are usually represented by conditional probabilities
among these vertices and are usually obtained from outside of the system.
 -connectedness is based on graph theory; however, graph theory only deals with vertices and edges with or without weights. In order to define a partial, incomplete, or fuzzy connectedness, one needs to assign a function on the vertex in the graph. Such a function is called a potential function. It can be used to represent the intensity of an image, the surface of a XY-domain, or the utility function of a management or economic network.
-connectedness is based on graph theory; however, graph theory only deals with vertices and edges with or without weights. In order to define a partial, incomplete, or fuzzy connectedness, one needs to assign a function on the vertex in the graph. Such a function is called a potential function. It can be used to represent the intensity of an image, the surface of a XY-domain, or the utility function of a management or economic network.
 -connectedness can be described as follows: a simple system
-connectedness can be described as follows: a simple system 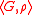 , where
, where 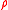 is called a potential function of
is called a potential function of  . If
. If  is an image, then
is an image, then  is a 2D or 2D grid space and
is a 2D or 2D grid space and  is an intensity function. For a color image, one can use
is an intensity function. For a color image, one can use  to represent
to represent 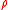 .
.
A neighbor connectivity will be first defined on a pair of adjacent points. Then one can define the general connectedness for any two points.
Assume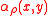 is used to measure the neighbor-connectivity of x,y where x and y are adjacent.
is used to measure the neighbor-connectivity of x,y where x and y are adjacent.
In graph G = (V, E), a finite sequence is called a path, if
is called a path, if 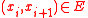 .
.
The path-connectivity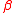 of a path
of a path 
is defined as
Finally, the degree of connectedness (connectivity) of two vertices x,y with respect to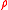 is defined as
is defined as
For a given , point
, point  and
and 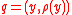 are said to be
are said to be  -connected if
-connected if 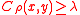 .
.
 -connectedness is a equivalence relation. It can be used in image segmentation.
-connectedness is a equivalence relation. It can be used in image segmentation.
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, lambda-connectedness (or λ-connectedness) deals with partial connectivity for a discrete space
Discrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
.
Assume that a function on a discrete space (usually a graph
Graph
Graph may refer to:* A graphic depicting the relationship between two or more variables used, for instance, in visualising scientific data.In mathematics:* Graph , is a set of vertices and edges....
) is given. A degree of connectivity (connectedness) will be defined to measure the connectedness of the space with respect to the function. It was invented to create a new method for image segmentation
Segmentation
Segmentation may mean:*Market segmentation, in economics and marketingBiology*A process of morphogenesis that divides a metazoan body into a series of semi-repetitive segments*Segmentation , a series of semi-repetitive segments...
. The method has expanded to handle other problems related to uncertainty for incomplete information analysis.
For a digital image and a certain value of
 , two pixels are called
, two pixels are called  -connected if there is a path linking those two pixels and the connectedness of this path is at least
-connected if there is a path linking those two pixels and the connectedness of this path is at least  .
.  -connectedness is an equivalence relation.
-connectedness is an equivalence relation.Background
Connectedness is a basic measure in many areas of mathematical science and social sciences. In graph theory, two vertices are said to be connected if there is a path between them. In topologyTopology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, two points are connected if there is a continuous
function that could move from one point to another continuously. In management science, for example, in an institution,
two individuals are connected if one person is under the supervision of the other. Such connected relations only describe either full connection or no connection. lambda-connectedness is introduced to measure incomplete or fuzzy relations between two vertices, points, human beings, etc.
In fact, partial relations have been studied in other aspects. Random graph
Random graph
In mathematics, a random graph is a graph that is generated by some random process. The theory of random graphs lies at the intersection between graph theory and probability theory, and studies the properties of typical random graphs.-Random graph models:...
theory allows one to assign a probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
to each edge of a graph. This method assumes, in most cases, each edge has the same probability. On the other hand, Bayesian networks are often used for inference and analysis when relationships between each pair of states/events, denoted by vertices, are known. These relationships are usually represented by conditional probabilities
among these vertices and are usually obtained from outside of the system.
 -connectedness is based on graph theory; however, graph theory only deals with vertices and edges with or without weights. In order to define a partial, incomplete, or fuzzy connectedness, one needs to assign a function on the vertex in the graph. Such a function is called a potential function. It can be used to represent the intensity of an image, the surface of a XY-domain, or the utility function of a management or economic network.
-connectedness is based on graph theory; however, graph theory only deals with vertices and edges with or without weights. In order to define a partial, incomplete, or fuzzy connectedness, one needs to assign a function on the vertex in the graph. Such a function is called a potential function. It can be used to represent the intensity of an image, the surface of a XY-domain, or the utility function of a management or economic network.Basic concepts
A generalized definition of -connectedness can be described as follows: a simple system
-connectedness can be described as follows: a simple system 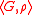 , where
, where 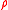 is called a potential function of
is called a potential function of  . If
. If  is an image, then
is an image, then  is a 2D or 2D grid space and
is a 2D or 2D grid space and  is an intensity function. For a color image, one can use
is an intensity function. For a color image, one can use  to represent
to represent 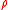 .
.A neighbor connectivity will be first defined on a pair of adjacent points. Then one can define the general connectedness for any two points.
Assume
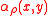 is used to measure the neighbor-connectivity of x,y where x and y are adjacent.
is used to measure the neighbor-connectivity of x,y where x and y are adjacent.In graph G = (V, E), a finite sequence
 is called a path, if
is called a path, if 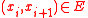 .
.The path-connectivity
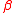 of a path
of a path 
is defined as
Finally, the degree of connectedness (connectivity) of two vertices x,y with respect to
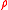 is defined as
is defined asFor a given
 , point
, point  and
and 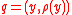 are said to be
are said to be  -connected if
-connected if 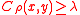 .
. -connectedness is a equivalence relation. It can be used in image segmentation.
-connectedness is a equivalence relation. It can be used in image segmentation.