Lagrange's theorem (number theory)
Encyclopedia
In number theory
, Lagrange's theorem states that:
If the modulus
is not prime, then it is possible for there to be more than n solutions. The exact number of solutions can be determined by finding the prime factorization of n. We then split the polynomial congruence into several polynomial congruences, one for each distinct prime factor, and find solutions modulo powers of the prime factors. Then, the number of solutions is equal to the product of the number of solutions for each individual congruence.
Lagrange's theorem is named after Joseph Lagrange
.
Assuming it is true for n = k, consider a non-zero polynomial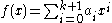
, deg(f) = k + 1, with m roots.
Without loss of generality m > 0, so there is an r such that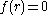
.
So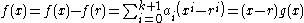
for some polynomial g with deg(g) = k. Clearly 
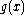is not identically zero, so 
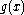has at most k roots.
Since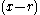
has precisely one root, 
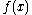has at most k + 1 roots and the proof is complete.
).
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, Lagrange's theorem states that:
- If p is a prime numberPrime numberA prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
and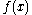
is an integer polynomial over 
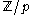of degree n and not identically equal to zero (with at least one coefficient not divisible by p), then 
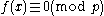has at most n solutions in 
.
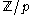If the modulus
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
is not prime, then it is possible for there to be more than n solutions. The exact number of solutions can be determined by finding the prime factorization of n. We then split the polynomial congruence into several polynomial congruences, one for each distinct prime factor, and find solutions modulo powers of the prime factors. Then, the number of solutions is equal to the product of the number of solutions for each individual congruence.
Lagrange's theorem is named after Joseph Lagrange
Joseph Lagrange
Count Joseph Lagrange was a French soldier who rose through the ranks and gained promotion to the rank of general officer during the French Revolutionary Wars, subsequently pursuing a successful career during the Napoleonic Wars and winning promotion to the top military rank of General of Division....
.
A proof of Lagrange's theorem
Proceed by induction on n, noting that it is trivially true for n = 0.Assuming it is true for n = k, consider a non-zero polynomial
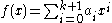, deg(f) = k + 1, with m roots.Without loss of generality m > 0, so there is an r such that
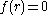.So
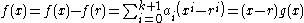for some polynomial g with deg(g) = k. Clearly 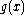is not identically zero, so 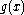has at most k roots.Since
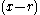has precisely one root, 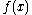has at most k + 1 roots and the proof is complete.Extension
The theorem and proof given above generalize to arbitrary fields, having multiplicative inverses for all non-zero elements (for example,).