Kuratowski's free set theorem
Encyclopedia
Kuratowski's free set theorem, named after Kazimierz Kuratowski
, is a result of set theory
, an area of mathematics
. It is a result which has been largely forgotten for almost 50 years, but has been applied recently in solving several lattice theory problems, such as the Congruence Lattice Problem
.
Denote by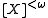
the set of all finite subsets of a set 
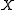. Likewise, for a positive integer 
, denote by 
the set of all 
-elements subsets of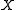 
. For a mapping
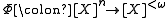, we say that a subset
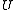of 
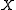is free (with respect to 
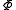), if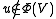 
, for any 
-element subset 
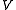of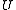 
and any 
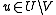. Kuratowski published in 1951 the following result, which characterizes the infinite cardinals
of the form
.
The theorem states the following. Let
be a positive integer and let 
be a set. Then the cardinality of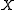 
is greater than or equal to 
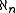if and only if for every mapping 
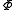from 
to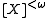 
,
there exists an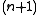
-element free subset of 
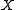with respect to 
.
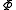For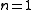
, Kuratowski's free set theorem is superseded by Hajnal's set mapping theorem.
Kazimierz Kuratowski
Kazimierz Kuratowski was a Polish mathematician and logician. He was one of the leading representatives of the Warsaw School of Mathematics.-Biography and studies:...
, is a result of set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, an area of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
. It is a result which has been largely forgotten for almost 50 years, but has been applied recently in solving several lattice theory problems, such as the Congruence Lattice Problem
Congruence lattice problem
In mathematics, the congruence lattice problem asks whether every algebraic distributive lattice is isomorphic to the congruence lattice of some other lattice. The problem was posed by Robert P. Dilworth, and for many years it was one of the most famous and long-standing open problems in lattice...
.
Denote by
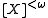the set of all finite subsets of a set 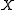. Likewise, for a positive integer , denote by the set of all -elements subsets of 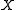. For a mappingMap (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
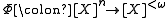, we say that a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
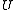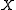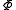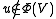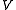of is free (with respect to ), if , for any -element subset of 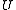and any 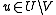. Kuratowski published in 1951 the following result, which characterizes the infinite cardinalsCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
of the form
.The theorem states the following. Let
be a positive integer and let be a set. Then the cardinality of 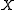is greater than or equal to 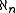if and only if for every mapping 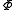from to 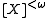,there exists an
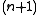-element free subset of 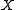with respect to 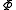.For
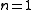, Kuratowski's free set theorem is superseded by Hajnal's set mapping theorem.