Kolmogorov's inequality
Encyclopedia
In probability theory
, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound. The inequality is named after the Russia
n mathematician
Andrey Kolmogorov
.
random variable
s defined on a common probability space
(Ω, F, Pr), with expected value
E[Xk] = 0 and variance
Var[Xk] < +∞ for k = 1, ..., n. Then, for each λ > 0,
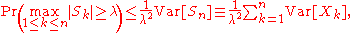
where Sk = X1 + ... + Xk.
s.
As argued in the discussion of Doob's martingale inequality
, the sequence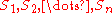
is a martingale.
Without loss of generality
, we can assume that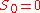
and 
for all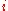 
.
Define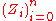
as follows. Let 
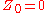, and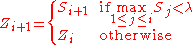
for all
.
Then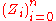
is a also a martingale. Since 
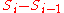is independent and mean zero,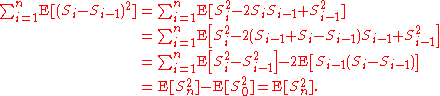
The same is true for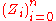
. Thus
by Chebyshev's inequality
.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Kolmogorov's inequality is a so-called "maximal inequality" that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound. The inequality is named after the Russia
Russia
Russia or , officially known as both Russia and the Russian Federation , is a country in northern Eurasia. It is a federal semi-presidential republic, comprising 83 federal subjects...
n mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Andrey Kolmogorov
Andrey Kolmogorov
Andrey Nikolaevich Kolmogorov was a Soviet mathematician, preeminent in the 20th century, who advanced various scientific fields, among them probability theory, topology, intuitionistic logic, turbulence, classical mechanics and computational complexity.-Early life:Kolmogorov was born at Tambov...
.
Statement of the inequality
Let X1, ..., Xn : Ω → R be independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s defined on a common probability space
Probability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
(Ω, F, Pr), with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
E[Xk] = 0 and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
Var[Xk] < +∞ for k = 1, ..., n. Then, for each λ > 0,
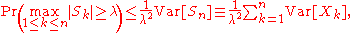
where Sk = X1 + ... + Xk.
Proof
The following argument is due to Kareem Amin and employs discrete martingaleMartingale
Martingale can refer to:*Martingale , a stochastic process in which the conditional expectation of the next value, given the current and preceding values, is the current value*Martingale for horses...
s.
As argued in the discussion of Doob's martingale inequality
Doob's martingale inequality
In mathematics, Doob's martingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a stochastic process exceeds any given value over a given interval of time...
, the sequence
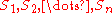is a martingale.Without loss of generality
Without loss of generality
Without loss of generality is a frequently used expression in mathematics...
, we can assume that
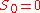and for all 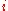.Define
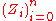as follows. Let 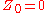, and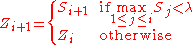for all
.Then
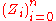is a also a martingale. Since 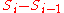is independent and mean zero,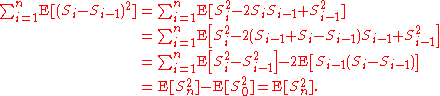The same is true for
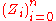. Thusby Chebyshev's inequality
Chebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
.
See also
- Chebyshev's inequalityChebyshev's inequalityIn probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
- Doob's martingale inequalityDoob's martingale inequalityIn mathematics, Doob's martingale inequality is a result in the study of stochastic processes. It gives a bound on the probability that a stochastic process exceeds any given value over a given interval of time...
- Etemadi's inequalityEtemadi's inequalityIn probability theory, Etemadi's inequality is a so-called "maximal inequality", an inequality that gives a bound on the probability that the partial sums of a finite collection of independent random variables exceed some specified bound...
- Landau–Kolmogorov inequality
- Markov's inequalityMarkov's inequalityIn probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
- Bernstein inequalities (probability theory)