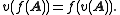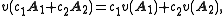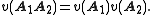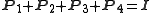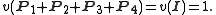Kochen-Specker theorem
Encyclopedia
In quantum mechanics
, the Kochen–Specker (KS) theorem is a "no go" theorem proved by Simon B. Kochen
and Ernst Specker
in 1967. It places certain constraints on the permissible types of hidden variable theories
which try to explain the apparent randomness of quantum mechanics
as a deterministic model featuring hidden states. The theorem is a complement to Bell's theorem
.
The theorem proves that there is a contradiction between two basic assumptions of the hidden variable theories intended to reproduce the results of quantum mechanics: that all hidden variables corresponding to quantum mechanical observables have definite values at any given time, and that the values of those variables are intrinsic and independent of the device used to measure them. The contradiction is caused by the fact that quantum mechanical observables need not be commutative
, making it impossible to embed the algebra
of these observables in a commutative algebra, assumed to represent the classical structure of the hidden variables theory.
The Kochen–Specker proof demonstrates the impossibility of Einstein's assumption, made in the famous Einstein–Podolsky–Rosen
paper, that quantum mechanical observables represent 'elements of physical reality'. More generally, the theorem excludes hidden variable theories
that require elements of physical reality to be non-contextual (i.e. independent of the measurement arrangement).
. This paradox is derived from the assumption that a quantum mechanical measurement result is generated in a deterministic way as a consequence of the existence of an element of physical reality
assumed to be present before the measurement as a property of the microscopic object. In the EPR paper it was assumed that the measured value of a quantum mechanical observable can play the role of such an element of physical reality. As a consequence of this metaphysical supposition the EPR criticism was not taken very seriously by the majority of the physics community. Moreover, in his answer Bohr had pointed to an ambiguity in the EPR paper, to the effect that it assumes the value of a quantum mechanical observable is non-contextual (i.e. is independent of the measurement arrangement). Taking into account the contextuality stemming from the measurement arrangement would, according to Bohr, make obsolete the EPR reasoning. It was subsequently observed by Einstein that Bohr's reliance on contextuality implies nonlocality ("spooky action at a distance"), and that, in consequence, one would have to accept incompleteness if one wanted to avoid nonlocality.
In the 1950s and '60s two lines of development were open for those not averse to metaphysics, both lines improving on a "no go" theorem presented by von Neumann
, purporting to prove the impossibility of the hidden variable theories yielding the same results as quantum mechanics. First, Bohm
developed an interpretation of quantum mechanics
, generally accepted as a hidden variable theory
underpinning quantum mechanics. The nonlocality of Bohm's theory induced Bell
to assume that quantum reality is nonlocal, and that probably only local hidden variable theories are in disagreement with quantum mechanics. More importantly, Bell managed to lift the problem from the level of metaphysics to physics by deriving an inequality, the Bell inequality
, that is capable of being experimentally tested.
A second line is the Kochen–Specker one. The essential difference from Bell's approach is that the possibility of underpinning quantum mechanics by a hidden variable theory is dealt with independently of any reference to
nonlocality. Although contextuality plays an important part, there is no implication of nonlocality because the proof refers to observables belonging to one single object, to be measured in one and the same region of space. Contextuality is related here with incompatibility of quantum mechanical observables, incompatibility being associated with mutual exclusiveness of measurement arrangements.
Considerably simpler proofs than the Kochen–Specker one were given later, amongst others, by Mermin
and by Peres
.
mechanical observables into a set of classical quantities,
notwithstanding that all classical quantities are mutually compatible.
The first observation made in the Kochen–Specker paper, is that this is possible in a trivial way, viz. by ignoring the algebraic structure of the set of quantum mechanical observables. Indeed, let pA(ak) be the probability that observable A has value ak, then the product ΠApA(ak), taken over all possible observables A, is a valid joint probability distribution, yielding all probabilities of quantum mechanical observables by taking marginals
. Kochen and Specker note that this joint probability distribution is not acceptable, however, since it ignores all correlations between the observables. Thus, in quantum mechanics A2 has value ak2 if A has value ak, implying that the values of A and A2 are highly correlated.
More generally it is required by Kochen and Specker that for an arbitrary function f the value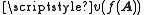
of observable 
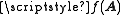satisfies
If A1 and A2 are compatible (commeasurable) observables, then, by the same token, we should have the following two equalities
and 
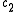real, and
The first of the latter two equalities is a considerable weakening compared to von Neumann's assumption that this equality should hold independently of whether A1 and A2 are compatible or incompatible. Kochen and Specker were capable of proving that a value assignment is not possible even on the basis of these weaker assumptions. In order to do so they restricted the observables to a special class, viz. so-called yes-no observables, having only values 0 and 1, corresponding to projection operators on the eigenvectors of certain orthogonal bases of a Hilbert space.
Restricting themselves to a three-dimensional Hilbert space, they were able to find a set of 117 such projection operators, not allowing to attribute to each of them in an unambiguous way either value 0 or 1. Instead of the rather involved proof by Kochen and Specker it is more illuminating to reproduce here one of the much simpler proofs given much later, which employs a lower number of projection operators by considering a four-dimensional Hilbert space. It turns out that it is possible to obtain a similar result on the basis of a set of only 18 projection operators. The method also works in an eight dimensional Hilbert Space.
In order to do so it is sufficient to realize that, if u1, u2, u3 and u4 are the four orthogonal vectors of an orthogonal basis in the four-dimensional Hilbert space, then the projection operators P1, P2, P3, P4 on these vectors are all mutually commuting (and, hence, correspond to compatible observables, allowing a simultaneous attribution of values 0 or 1). Since
it follows that
But, since
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, the Kochen–Specker (KS) theorem is a "no go" theorem proved by Simon B. Kochen
Simon B. Kochen
Simon Bernhard Kochen is an American mathematician, working in the fields of model theory, number theory and quantum mechanics....
and Ernst Specker
Ernst Specker
Ernst P. Specker is a Swiss mathematician. Much of his most influential work has been on Quine’s New Foundations, a set theory with a universal set, but he is most famous for the Kochen–Specker theorem in quantum mechanics, showing that certain types of hidden variable theories are impossible...
in 1967. It places certain constraints on the permissible types of hidden variable theories
Hidden variable theory
Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation...
which try to explain the apparent randomness of quantum mechanics
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
as a deterministic model featuring hidden states. The theorem is a complement to Bell's theorem
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
.
The theorem proves that there is a contradiction between two basic assumptions of the hidden variable theories intended to reproduce the results of quantum mechanics: that all hidden variables corresponding to quantum mechanical observables have definite values at any given time, and that the values of those variables are intrinsic and independent of the device used to measure them. The contradiction is caused by the fact that quantum mechanical observables need not be commutative
Commutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
, making it impossible to embed the algebra
Algebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
of these observables in a commutative algebra, assumed to represent the classical structure of the hidden variables theory.
The Kochen–Specker proof demonstrates the impossibility of Einstein's assumption, made in the famous Einstein–Podolsky–Rosen
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
paper, that quantum mechanical observables represent 'elements of physical reality'. More generally, the theorem excludes hidden variable theories
Hidden variable theory
Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation...
that require elements of physical reality to be non-contextual (i.e. independent of the measurement arrangement).
History
The KS theorem is an important step in the debate on the (in)completeness of quantum mechanics, boosted in 1935 by the criticism in the EPR paper of the Copenhagen assumption of completeness, creating the so-called EPR paradoxEPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
. This paradox is derived from the assumption that a quantum mechanical measurement result is generated in a deterministic way as a consequence of the existence of an element of physical reality
EPR paradox
The EPR paradox is a topic in quantum physics and the philosophy of science concerning the measurement and description of microscopic systems by the methods of quantum physics...
assumed to be present before the measurement as a property of the microscopic object. In the EPR paper it was assumed that the measured value of a quantum mechanical observable can play the role of such an element of physical reality. As a consequence of this metaphysical supposition the EPR criticism was not taken very seriously by the majority of the physics community. Moreover, in his answer Bohr had pointed to an ambiguity in the EPR paper, to the effect that it assumes the value of a quantum mechanical observable is non-contextual (i.e. is independent of the measurement arrangement). Taking into account the contextuality stemming from the measurement arrangement would, according to Bohr, make obsolete the EPR reasoning. It was subsequently observed by Einstein that Bohr's reliance on contextuality implies nonlocality ("spooky action at a distance"), and that, in consequence, one would have to accept incompleteness if one wanted to avoid nonlocality.
In the 1950s and '60s two lines of development were open for those not averse to metaphysics, both lines improving on a "no go" theorem presented by von Neumann
John von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
, purporting to prove the impossibility of the hidden variable theories yielding the same results as quantum mechanics. First, Bohm
David Bohm
David Joseph Bohm FRS was an American-born British quantum physicist who contributed to theoretical physics, philosophy, neuropsychology, and the Manhattan Project.-Youth and college:...
developed an interpretation of quantum mechanics
Bohm interpretation
The de Broglie–Bohm theory, also called the pilot-wave theory, Bohmian mechanics, and the causal interpretation, is an interpretation of quantum theory. In addition to a wavefunction on the space of all possible configurations, it also includes an actual configuration, even in situations where...
, generally accepted as a hidden variable theory
Hidden variable theory
Historically, in physics, hidden variable theories were espoused by some physicists who argued that quantum mechanics is incomplete. These theories argue against the orthodox interpretation of quantum mechanics, which is the Copenhagen Interpretation...
underpinning quantum mechanics. The nonlocality of Bohm's theory induced Bell
John Stewart Bell
John Stewart Bell FRS was a British physicist from Northern Ireland , and the originator of Bell's theorem, a significant theorem in quantum physics regarding hidden variable theories.- Early life and work :...
to assume that quantum reality is nonlocal, and that probably only local hidden variable theories are in disagreement with quantum mechanics. More importantly, Bell managed to lift the problem from the level of metaphysics to physics by deriving an inequality, the Bell inequality
Bell's theorem
In theoretical physics, Bell's theorem is a no-go theorem, loosely stating that:The theorem has great importance for physics and the philosophy of science, as it implies that quantum physics must necessarily violate either the principle of locality or counterfactual definiteness...
, that is capable of being experimentally tested.
A second line is the Kochen–Specker one. The essential difference from Bell's approach is that the possibility of underpinning quantum mechanics by a hidden variable theory is dealt with independently of any reference to
nonlocality. Although contextuality plays an important part, there is no implication of nonlocality because the proof refers to observables belonging to one single object, to be measured in one and the same region of space. Contextuality is related here with incompatibility of quantum mechanical observables, incompatibility being associated with mutual exclusiveness of measurement arrangements.
Considerably simpler proofs than the Kochen–Specker one were given later, amongst others, by Mermin
David Mermin
Nathaniel David Mermin is a solid-state physicist at Cornell University best known for the eponymous Mermin-Wagner theorem and his application of the term "Boojum" to superfluidity, and for the quote "Shut up and calculate!"Together with Neil W...
and by Peres
Asher Peres
Asher Peres was an Israeli physicist, considered a pioneer in quantum information theory. According to his autobiography, he was born in Beaulieu-sur-Dordogne in France, where his father, a Polish electrical engineer, had found work laying down power lines...
.
The KS theorem
The KS theorem explores whether it is possible to embed the set of quantummechanical observables into a set of classical quantities,
notwithstanding that all classical quantities are mutually compatible.
The first observation made in the Kochen–Specker paper, is that this is possible in a trivial way, viz. by ignoring the algebraic structure of the set of quantum mechanical observables. Indeed, let pA(ak) be the probability that observable A has value ak, then the product ΠApA(ak), taken over all possible observables A, is a valid joint probability distribution, yielding all probabilities of quantum mechanical observables by taking marginals
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
. Kochen and Specker note that this joint probability distribution is not acceptable, however, since it ignores all correlations between the observables. Thus, in quantum mechanics A2 has value ak2 if A has value ak, implying that the values of A and A2 are highly correlated.
More generally it is required by Kochen and Specker that for an arbitrary function f the value
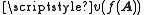of observable 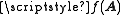satisfies
If A1 and A2 are compatible (commeasurable) observables, then, by the same token, we should have the following two equalities
and 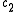real, and
The first of the latter two equalities is a considerable weakening compared to von Neumann's assumption that this equality should hold independently of whether A1 and A2 are compatible or incompatible. Kochen and Specker were capable of proving that a value assignment is not possible even on the basis of these weaker assumptions. In order to do so they restricted the observables to a special class, viz. so-called yes-no observables, having only values 0 and 1, corresponding to projection operators on the eigenvectors of certain orthogonal bases of a Hilbert space.
Restricting themselves to a three-dimensional Hilbert space, they were able to find a set of 117 such projection operators, not allowing to attribute to each of them in an unambiguous way either value 0 or 1. Instead of the rather involved proof by Kochen and Specker it is more illuminating to reproduce here one of the much simpler proofs given much later, which employs a lower number of projection operators by considering a four-dimensional Hilbert space. It turns out that it is possible to obtain a similar result on the basis of a set of only 18 projection operators. The method also works in an eight dimensional Hilbert Space.
In order to do so it is sufficient to realize that, if u1, u2, u3 and u4 are the four orthogonal vectors of an orthogonal basis in the four-dimensional Hilbert space, then the projection operators P1, P2, P3, P4 on these vectors are all mutually commuting (and, hence, correspond to compatible observables, allowing a simultaneous attribution of values 0 or 1). Since
it follows that
But, since
-
-
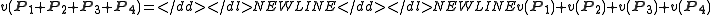
it follows from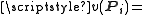
0 or 1, 
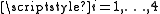, that out of the four values 
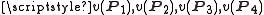, one must be 1 while the other three must be 0.
Cabello, extending an argument developed by Kernaghan considered 9 orthogonal bases, each basis corresponding to a column of the following table, in which the basis vectors are explicitly displayed. The bases are chosen in such a way that each has a vector in common with one other basis (indicated in the table by equal colours), thus establishing certain correlations between the 36 corresponding yes-no observables.
u1 (0, 0, 0, 1) (0, 0, 0, 1) (1, –1, 1, –1) (1, –1, 1, –1) (0, 0, 1, 0) (1, –1, –1, 1) (1, 1, –1, 1) (1, 1, –1, 1) (1, 1, 1, –1) u2 (0, 0, 1, 0) (0, 1, 0, 0) (1, –1, –1, 1) (1, 1, 1, 1) (0, 1, 0, 0) (1, 1, 1, 1) (1, 1, 1, –1) (–1, 1, 1, 1) (–1, 1, 1, 1) u3 (1, 1, 0, 0) (1, 0, 1, 0) (1, 1, 0, 0) (1, 0, –1, 0) (1, 0, 0, 1) (1, 0, 0, –1) (1, –1, 0, 0) (1, 0, 1, 0) (1, 0, 0, 1) u4 (1, –1, 0, 0) (1, 0, –1, 0) (0, 0, 1, 1) (0, 1, 0, –1) (1, 0, 0, –1) (0, 1, –1, 0) (0, 0, 1, 1) (0, 1, 0, –1) (0, 1, –1, 0)
Now the "no go" theorem easily follows by making sure that it is impossible to
distribute the four numbers 1,0,0,0 over the four rows of each column, such that
equally coloured compartments contain equal numbers. Another way to see the theorem, using the approach by Kernaghan, is to recognize that a contradiction is implied between the odd number of bases and the even number of occurrences of the observables.
Remarks on the KS theorem
1. Contextuality
In the Kochen–Specker paper the possibility is discussed that the value attribution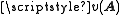
may be context-dependent, i.e. observables corresponding to equal vectors in different columns of the table need not have equal values because different columns correspond to different measurement arrangements. Since subquantum reality (as described by the hidden variable theory) may be dependent on the measurement context, it is possible that relations between quantum mechanical observables and hidden variables are just homomorphic rather than isomorphic. This would make obsolete the requirement of a context-independent value attribution. Hence, the KS theorem does only exclude noncontextual hidden variable theories. The possibility of contextuality has given rise to the so-called modal interpretations of quantum mechanics.
2. Different levels of description
By the KS theorem the impossibility is proven of Einstein's assumption that an element of physical reality is represented by a value of a quantum mechanical observable. The question may be asked whether this is a very shocking result. The value of a quantum mechanical observable refers in the first place to the final position of the pointer of a measuring instrument, which comes into being only during the measurement, and which, for this reason, cannot play the role of an element of physical reality. Elements of physical reality, if existing, would seem to need a subquantum (hidden variable) theory for their description
rather than quantum mechanics. In later publications the Bell inequalities are discussed on the basis of hidden variable theories in which the hidden variable is supposed to refer to a subquantum property of the microscopic object different from the value of a quantum mechanical observable. This opens up the possibility of distinguishing different levels of reality described by different theories, which, incidentally, had already been practised by Louis de Broglie. For such more general theories the KS theorem is applicable only if the measurement is assumed to be a faithful one, in the sense that there is a deterministic relation between a subquantum element of physical reality and the value of the observable found on measurement. The existence or nonexistence of such subquantum elements of physical reality is not touched by the KS theorem. As an example, recent experiments on bouncing drops on a vibrating bath, by Y. Couder and collaborators, reproduce many features of quantum mechanics . In this case, the subquantum elements of physical reality are linked to the specifics of the hydrodynamics of bouncing drops on a vibrating bath (linked to the Faraday waveFaraday waveFaraday waves, also known as Faraday ripples, named after Michael Faraday, are nonlinear standing waves that appear on liquids enclosed by a vibrating receptacle. When the vibration frequency exceeds a critical value, the flat hydrostatic surface becomes unstable. This is known as the Faraday...
instability phenomenology ). At the level that reproduces features of quantum mechanics, measurement are not deterministic since they depend on the stochasticStochasticStochastic refers to systems whose behaviour is intrinsically non-deterministic. A stochastic process is one whose behavior is non-deterministic, in that a system's subsequent state is determined both by the process's predictable actions and by a random element. However, according to M. Kac and E...
nature of the non-linear dynamics of the subquantum elements. The experiments are indeed interpreted in the framework of De Broglie–Bohm theory of pilot waves.
External links
- Carsten Held, The Kochen–Specker Theorem, Stanford Encyclopedia of Philosophy *http://plato.stanford.edu/entries/kochen-specker/
- Kochen-Specker theorem on arxiv.org
- S. Kochen and E. P. Specker, The problem of hidden variables in quantum mechanics, Full text http://www.iumj.indiana.edu/IUMJ/dfulltext.php?year=1968&volume=17&artid=17004
-