
Knuth's Algorithm X
Encyclopedia
Donald Knuth
's Algorithm X is a recursive
, nondeterministic
, depth-first, backtracking
algorithm
that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s. The goal is to select a subset of the rows so that the digit 1 appears in each column exactly once.
Algorithm X functions as follows:
The nondeterministic choice of r means that the algorithm essentially clones itself into independent subalgorithms; each subalgorithm inherits the current matrix A, but reduces it with respect to a different row r.
If column c is entirely zero, there are no subalgorithms and the process terminates unsuccessfully.
The subalgorithms form a search tree
in a natural way, with the original problem at the root and with level k containing each subalgorithm that corresponds to k chosen rows.
Backtracking is the process of traversing the tree in preorder, depth first.
Any systematic rule for choosing column c in this procedure will find all solutions, but some rules work much better than others.
To reduce the number of iterations, Knuth
suggests that the column choosing algorithm select a column with the lowest number of 1s in it.
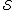 = {A, B, C, D, E, F}, where:
= {A, B, C, D, E, F}, where:
This problem is represented by the matrix:
Algorithm X with Knuth's suggested heuristic for selecting columns solves this problem as follows:
Level 0
Step 1—The matrix is not empty, so the algorithm proceeds.
Step 2—The lowest number of 1s in any column is two. Column 1 is the first column with two 1s and thus is selected (deterministically):
Step 3—Rows A and B each have a 1 in column 1 and thus are selected (nondeterministically).
The algorithm moves to the first branch at level 1…
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
! !! 2 !! 3 !! 5 !! 6
|-
! D
| 0 || 1 || 1 || 1
|}
! !! 2 !! 3 !! 5 !! 6
|-
! D
| 0 || 1 || 1 || 1
|}
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
! !! 2 !! 7
|-
! F
| 1 || 1
|}
! !! 2 !! 7
|-
! F
| 1 || 1
|}
! !! 2 !! 7
|-
! F
| 1 || 1
|}
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
There are no branches at level 0, thus the algorithm terminates.
In summary, the algorithm determines there is only one exact cover: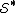 = {B, D, F}.
= {B, D, F}.
, commonly known as DLX, is the technique suggested by Knuth
to efficiently implement his Algorithm X on a computer. Dancing Links implements the matrix using circular doubly linked lists of the 1s in the matrix. There is a list of 1s for each row and each column. Each 1 in the matrix has a link to the next 1 above, below, to the left, and to the right of itself.
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
's Algorithm X is a recursive
Recursion (computer science)
Recursion in computer science is a method where the solution to a problem depends on solutions to smaller instances of the same problem. The approach can be applied to many types of problems, and is one of the central ideas of computer science....
, nondeterministic
Nondeterministic algorithm
In computer science, a nondeterministic algorithm is an algorithm that can exhibit different behaviors on different runs, as opposed to a deterministic algorithm. There are several ways an algorithm may behave differently from run to run. A concurrent algorithm can perform differently on different...
, depth-first, backtracking
Backtracking
Backtracking is a general algorithm for finding all solutions to some computational problem, that incrementally builds candidates to the solutions, and abandons each partial candidate c as soon as it determines that c cannot possibly be completed to a valid solution.The classic textbook example...
algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
that finds all solutions to the exact cover problem represented by a matrix A consisting of 0s and 1s. The goal is to select a subset of the rows so that the digit 1 appears in each column exactly once.
Algorithm X functions as follows:
|
The nondeterministic choice of r means that the algorithm essentially clones itself into independent subalgorithms; each subalgorithm inherits the current matrix A, but reduces it with respect to a different row r.
If column c is entirely zero, there are no subalgorithms and the process terminates unsuccessfully.
The subalgorithms form a search tree
Search tree
In computer science, a search tree is a binary tree data structure in whose nodes data values are stored from some ordered set, in such a way that in-order traversal of the tree visits the nodes in ascending order of the stored values...
in a natural way, with the original problem at the root and with level k containing each subalgorithm that corresponds to k chosen rows.
Backtracking is the process of traversing the tree in preorder, depth first.
Any systematic rule for choosing column c in this procedure will find all solutions, but some rules work much better than others.
To reduce the number of iterations, Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
suggests that the column choosing algorithm select a column with the lowest number of 1s in it.
Example
For example, consider the exact cover problem specified by the universe U = {1, 2, 3, 4, 5, 6, 7} and the collection of sets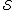 = {A, B, C, D, E, F}, where:
= {A, B, C, D, E, F}, where:
- A = {1, 4, 7};
- B = {1, 4};
- C = {4, 5, 7};
- D = {3, 5, 6};
- E = {2, 3, 6, 7}; and
- F = {2, 7}.
This problem is represented by the matrix:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| B | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| D | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| E | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| F | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Algorithm X with Knuth's suggested heuristic for selecting columns solves this problem as follows:
Level 0
Step 1—The matrix is not empty, so the algorithm proceeds.
Step 2—The lowest number of 1s in any column is two. Column 1 is the first column with two 1s and thus is selected (deterministically):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| A | 1 | 0 | 0 | 1 | 0 | 0 | 1 |
| B | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 1 | 0 | 1 |
| D | 0 | 0 | 1 | 0 | 1 | 1 | 0 |
| E | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| F | 0 | 1 | 0 | 0 | 0 | 0 | 1 |
Step 3—Rows A and B each have a 1 in column 1 and thus are selected (nondeterministically).
The algorithm moves to the first branch at level 1…
- Level 1: Select Row A
- Step 4—Row A is included in the partial solution.
- Step 5—Row A has a 1 in columns 1, 4, and 7:
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
- Column 1 has a 1 in rows
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
- Row
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 2 !! 3 !! 5 !! 6
|-
! D
| 0 || 1 || 1 || 1
|}
- Step 1—The matrix is not empty, so the algorithm proceeds.
- Step 2—The lowest number of 1s in any column is zero and column 2 is the first column with zero 1s:
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 2 !! 3 !! 5 !! 6
|-
! D
| 0 || 1 || 1 || 1
|}
- Thus this branch of the algorithm terminates unsuccessfully.
- The algorithm moves to the next branch at level 1…
- Level 1: Select Row
- Step 4—Row B is included in the partial solution.
- Row B has a 1 in columns 1 and 4:
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
- Column 1 has a 1 in rows A and B; and column 4 has a 1 in rows A, B, and C. Thus rows A, B, and C are to be removed and columns 1 and 4 are to be removed:
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! A
| 1 || 0 || 0 || 1 || 0 || 0 || 1
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! C
| 0 || 0 || 0 || 1 || 1 || 0 || 1
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! E
| 0 || 1 || 1 || 0 || 0 || 1 || 1
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
- Rows D, E, and F remain and columns 2, 3, 5, 6, and 7 remain:
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
- Step 1—The matrix is not empty, so the algorithm proceeds.
- Step 2—The lowest number of 1s in any column is one. Column 5 is the first column with one 1 and thus is selected (deterministically):
-
- {| border="1" cellpadding="5" cellspacing="0"
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
- Step 3—Row D has a 1 in column 5 and thus is selected (nondeterministically).
- The algorithm moves to the first branch at level 2…
-
- Level 2: Select Row D
-
- Step 4—Row D is included in the partial solution.
-
- Step 5—Row D has a 1 in columns 3, 5, and 6:
-
-
- {| border="1" cellpadding="5" cellspacing="0"
-
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
-
- Column 3 has a 1 in rows
-
-
- {| border="1" cellpadding="5" cellspacing="0"
-
! !! 2 !! 3 !! 5 !! 6 !! 7
|-
! D
| 0 || 1 || 1 || 1 || 0
|-
! E
| 1 || 1 || 0 || 1 || 1
|-
! F
| 1 || 0 || 0 || 0 || 1
|}
-
- Row
-
-
- {| border="1" cellpadding="5" cellspacing="0"
-
! !! 2 !! 7
|-
! F
| 1 || 1
|}
-
- Step 1—The matrix is not empty, so the algorithm proceeds.
-
- Step 2—The lowest number of 1s in any column is one. Column 2 is the first column with one 1 and thus is selected (deterministically).
-
- Row
-
- The algorithm moves to the first branch at level 3…
-
-
- Level 3: Select Row
-
-
-
- Step 4—Row F is included in the partial solution.
-
-
-
- Row F has a 1 in columns 2 and 7:
-
-
-
-
- {| border="1" cellpadding="5" cellspacing="0"
-
-
! !! 2 !! 7
|-
! F
| 1 || 1
|}
-
-
- Column 2 has a 1 in row F; and column 7 has a 1 in row F. Thus row F is to be removed and columns 2 and 7 are to be removed:
-
-
-
-
- {| border="1" cellpadding="5" cellspacing="0"
-
-
! !! 2 !! 7
|-
! F
| 1 || 1
|}
-
-
- Step 1—The matrix is empty, thus this branch of the algorithm terminates successfully.
-
-
-
- As rows B, D, and F are selected, the final solution is:
-
-
-
-
- {| border="1" cellpadding="5" cellspacing="0"
-
-
! !! 1 !! 2 !! 3 !! 4 !! 5 !! 6 !! 7
|-
! B
| 1 || 0 || 0 || 1 || 0 || 0 || 0
|-
! D
| 0 || 0 || 1 || 0 || 1 || 1 || 0
|-
! F
| 0 || 1 || 0 || 0 || 0 || 0 || 1
|}
-
-
- In other words, the subcollection {B, D, F} is an exact cover, since every element is contained in exactly one of the sets B = {1, 4}, D = {3, 5, 6}, or F = {2, 7}.
-
-
-
- There are no more selected rows at level 3, thus the algorithm moves to the next branch at level 2…
-
-
- There are no more selected rows at level 2, thus the algorithm moves to the next branch at level 1…
- There are no more selected rows at level 1, thus the algorithm moves to the next branch at level 0…
There are no branches at level 0, thus the algorithm terminates.
In summary, the algorithm determines there is only one exact cover:
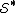 = {B, D, F}.
= {B, D, F}.Implementations
Dancing LinksDancing Links
In computer science, Dancing Links, also known as DLX, is the technique suggested by Donald Knuth to efficiently implement his Algorithm X. Algorithm X is a recursive, nondeterministic, depth-first, backtracking algorithm that finds all solutions to the exact cover problem...
, commonly known as DLX, is the technique suggested by Knuth
Donald Knuth
Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...
to efficiently implement his Algorithm X on a computer. Dancing Links implements the matrix using circular doubly linked lists of the 1s in the matrix. There is a list of 1s for each row and each column. Each 1 in the matrix has a link to the next 1 above, below, to the left, and to the right of itself.
External links
- Implementation of an Exact Cover solver in C# - uses Algorithm X and the Dancing Links optimization.
- Polycube solver Program (with Lua source code) to fill boxes with polycubes using Algorithm X.
- Knuth's Paper describing the Dancing Links optimization - Gzip'd postscript file.

