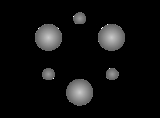
Klemperer rosette
Encyclopedia
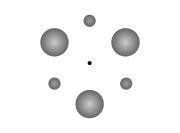
Barycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
. It was first described by W. B. Klemperer in 1962.
Klemperer described the system as follows:
The simplest rosette would be series of four alternating heavier and lighter bodies, 90 degrees from one another, in a rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
configuration [Heavy, Light, Heavy, Light], where the two heavier masses weigh the same, and likewise the two lighter masses weigh the same. The number of "mass types" can be increased, so long as the arrangement pattern is cylic: e.g. [ 1,2,3 ... 1,2,3 ], [ 1,2,3,4,5 ... 1,2,3,4,5 ], [ 1,2,3,3,2,1 ... 1,2,3,3,2,1 ] etc.
Klemperer also mentioned octagonal and rhombic
Rhombus
In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...
rosettes.
Misuse and misspelling
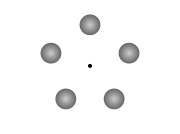
Equilateral
In geometry, an equilateral polygon is a polygon which has all sides of the same length.For instance, an equilateral triangle is a triangle of equal edge lengths...
polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
and given an equal angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
about their center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
.
Klemperer does indeed mention this configuration at the start of his article, but only as an already known set of equilibrium systems before introducing the actual rosettes.
In Larry Niven
Larry Niven
Laurence van Cott Niven / ˈlæri ˈnɪvən/ is an American science fiction author. His best-known work is Ringworld , which received Hugo, Locus, Ditmar, and Nebula awards. His work is primarily hard science fiction, using big science concepts and theoretical physics...
's novel Ringworld
Ringworld
Ringworld is a Hugo, Nebula, and Locus award-winning 1970 science fiction novel by Larry Niven, set in his Known Space universe and considered a classic of science fiction literature. It is followed by three sequels, and preceded by four prequels, and ties into numerous other books set in Known Space...
, the Puppeteers'
Pierson's Puppeteer
Pierson's Puppeteers, often known just as Puppeteers, are a fictional alien race from American author Larry Niven's Known Space books.- Biology and sociology :...
"Fleet of Worlds
Fleet of Worlds
Fleet of Worlds are both a location and a book in Larry Niven's Known Space series.The series consisting of this book and its sequels is referred to by the same title.-Novel:The novel, co-written by Niven and Edward M. Lerner, was released in 2007...
" is arranged in such a configuration (5 planets spaced at the points of a pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
) which Niven calls a "Kemplerer rosette"; this (possibly intentional) mis-spelling (and misuse) is one possible source of this confusion. Another is the similarity between Klemperer's name and that of Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
, who described certain laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
in the 17th century.
Instability
Simulations of this system (or a simple linear perturbation analysis) demonstrate that such systems are definitely not stable: any motion away from the perfect geometric configuration causes an oscillation, eventually leading to the disruption of the system (Klemperer's original article also states this fact). This is the case whether the center of the Rosette is in free space, or itself in orbit around a star. The short-form reason is that any perturbation destroys the symmetry, which increases the perturbation, which further damages the symmetry, and so on.The longer explanation is that any tangential perturbation causes a body to get closer to one neighbor and farther from another; the gravitational force becomes greater towards the closer neighbor and less for the farther neighbor, pulling the perturbed object further towards its closer neighbor, enhancing the perturbation rather than damping it. An inward radial perturbation causes the perturbed body to get closer to all other objects, increasing the force on the object and increasing its orbital velocity---which leads indirectly to a tangential perturbation and the argument above (a similar argument is used to demonstrate the orbital instability of the Ringworld itself, countered with artificial stabilisation techniques). Thus there is no doubt that the Puppeteers's Rosette of farming worlds, as described in Niven's Ringworld, would also require some form of artificial stabilizing.

