
Kazamaki's condition
Encyclopedia
Kazamaki's condition gives a sufficient criterion ensuring that the Doléans-Dade exponential
of a local martingale
is a true martingale
. In mathematics, this is particularly important if one wishes to apply Girsanov's theorem
in order to perform a change of measure
. Kazamaki's condition is more general than Novikov's condition
.
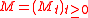 be a continuous local martingale with respect to a right-continuous filtration
be a continuous local martingale with respect to a right-continuous filtration  . If
. If 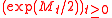 is a uniformly integrable submartingale, then the Doléans-Dade exponential (M) of M is a uniformly integrable martingale.
is a uniformly integrable submartingale, then the Doléans-Dade exponential (M) of M is a uniformly integrable martingale.
Doléans-Dade exponential
In stochastic calculus, the Doléans-Dade exponential, Doléans exponential, or stochastic exponential, of a semimartingale X is defined to be the solution to the stochastic differential equation with initial condition . The concept is named after Catherine Doléans-Dade...
of a local martingale
Local martingale
In mathematics, a local martingale is a type of stochastic process, satisfying the localized version of the martingale property. Every martingale is a local martingale; every bounded local martingale is a martingale; however, in general a local martingale is not a martingale, because its...
is a true martingale
Martingale (probability theory)
In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
. In mathematics, this is particularly important if one wishes to apply Girsanov's theorem
Girsanov theorem
In probability theory, the Girsanov theorem describes how the dynamics of stochastic processes change when the original measure is changed to an equivalent probability measure...
in order to perform a change of measure
Measure
- Legal :* Measure of the Church of England is a law passed by the General Synod and the UK Parliament equivalent of an Act* Measure of the National Assembly for Wales, a law specific to Wales passed by the Welsh Assembly between 2007 and 2011...
. Kazamaki's condition is more general than Novikov's condition
Novikov's condition
In probability theory, Novikov's condition is the sufficient condition for a stochastic process which takes the form of the Radon-Nikodym derivative in Girsanov's theorem to be a martingale...
.
Statement of Kazamaki's condition
Let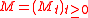 be a continuous local martingale with respect to a right-continuous filtration
be a continuous local martingale with respect to a right-continuous filtration  . If
. If 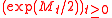 is a uniformly integrable submartingale, then the Doléans-Dade exponential (M) of M is a uniformly integrable martingale.
is a uniformly integrable submartingale, then the Doléans-Dade exponential (M) of M is a uniformly integrable martingale.

