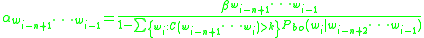Katz's back-off model
Encyclopedia
Katz back-off is a generative n-gram
language model
that estimates the conditional probability
of a word given its history in the n-gram. It accomplishes this estimation by "backing-off" to models with smaller histories under certain conditions. By doing so, the model with the most reliable information about a given history is used to provide the better results.
where, = number of times x appears in training
= number of times x appears in training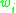 = ith word in the given context
= ith word in the given context
Essentially, this means that if the n-gram has been seen more than k times in training, the conditional probability of a word given its history is proportional to the maximum likelihood
estimate of that n-gram. Otherwise, the conditional probability is equal to the back-off conditional probability of the "(n-1)-gram".
The more difficult part is determining the values for k, d and α.
d is typically the amount of discounting found by Good-Turing estimation. In other words, if Good-Turing estimates as
as 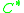 , then
, then 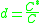
To compute α, it is useful to first define a quantity β, which is the left-over probability mass for the (n-1)-gram:
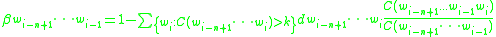
Then the back-off weight, α, is computed as follows: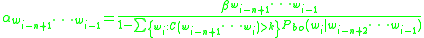
N-gram
In the fields of computational linguistics and probability, an n-gram is a contiguous sequence of n items from a given sequence of text or speech. The items in question can be phonemes, syllables, letters, words or base pairs according to the application...
language model
Language model
A statistical language model assigns a probability to a sequence of m words P by means of a probability distribution.Language modeling is used in many natural language processing applications such as speech recognition, machine translation, part-of-speech tagging, parsing and information...
that estimates the conditional probability
Conditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of a word given its history in the n-gram. It accomplishes this estimation by "backing-off" to models with smaller histories under certain conditions. By doing so, the model with the most reliable information about a given history is used to provide the better results.
The method
The equation for Katz's back-off model is deceptively simple: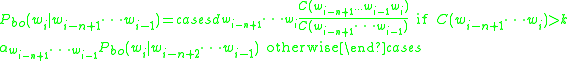
where,
 = number of times x appears in training
= number of times x appears in training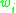 = ith word in the given context
= ith word in the given contextEssentially, this means that if the n-gram has been seen more than k times in training, the conditional probability of a word given its history is proportional to the maximum likelihood
Maximum likelihood
In statistics, maximum-likelihood estimation is a method of estimating the parameters of a statistical model. When applied to a data set and given a statistical model, maximum-likelihood estimation provides estimates for the model's parameters....
estimate of that n-gram. Otherwise, the conditional probability is equal to the back-off conditional probability of the "(n-1)-gram".
The more difficult part is determining the values for k, d and α.
Computing the parameters
k is the least important of the parameters. It is usually chosen to be 0. However, empirical testing may find better values for k.d is typically the amount of discounting found by Good-Turing estimation. In other words, if Good-Turing estimates
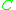 as
as 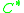 , then
, then 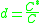
To compute α, it is useful to first define a quantity β, which is the left-over probability mass for the (n-1)-gram:
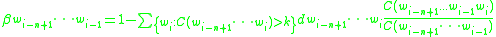
Then the back-off weight, α, is computed as follows: