
Kato theorem
Encyclopedia
The Kato theorem, or Kato's theorem, is used in computational quantum physics
. It states that for generalized Coulomb potentials, the electron density
has a cusp
at the position of the nuclei, where it satisfies
Here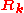 denotes the positions of the nuclei,
denotes the positions of the nuclei, 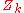 their atomic number
their atomic number
and is the Bohr radius
is the Bohr radius
.
For a Coulombic system one can thus, in principle, read off all information necessary for completely specifying the Hamiltonian directly from examining the density distribution. This is also known as E. Bright Wilson's argument within the framework of density functional theory
(DFT). The electron density of the ground state of a molecular system contains cusps
at the location of the nuclei, and by identifying these from the total electron density of the system, the positions are thus established. From Kato's theorem, one also obtains the nuclear charge of the nuclei, and thus the external potential is fully defined. Finally, integrating the electron density over space gives the number of electrons, and the (electronic) Hamiltonian
is defined. This is valid in a non-relativistic treatment within the Born-Oppenheimer approximation
, and assuming point-like nuclei.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
. It states that for generalized Coulomb potentials, the electron density
Electron density
Electron density is the measure of the probability of an electron being present at a specific location.In molecules, regions of electron density are usually found around the atom, and its bonds...
has a cusp
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
at the position of the nuclei, where it satisfies

Here
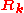 denotes the positions of the nuclei,
denotes the positions of the nuclei, 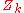 their atomic number
their atomic numberAtomic number
In chemistry and physics, the atomic number is the number of protons found in the nucleus of an atom and therefore identical to the charge number of the nucleus. It is conventionally represented by the symbol Z. The atomic number uniquely identifies a chemical element...
and
 is the Bohr radius
is the Bohr radiusBohr radius
The Bohr radius is a physical constant, approximately equal to the most probable distance between the proton and electron in a hydrogen atom in its ground state. It is named after Niels Bohr, due to its role in the Bohr model of an atom...
.
For a Coulombic system one can thus, in principle, read off all information necessary for completely specifying the Hamiltonian directly from examining the density distribution. This is also known as E. Bright Wilson's argument within the framework of density functional theory
Density functional theory
Density functional theory is a quantum mechanical modelling method used in physics and chemistry to investigate the electronic structure of many-body systems, in particular atoms, molecules, and the condensed phases. With this theory, the properties of a many-electron system can be determined by...
(DFT). The electron density of the ground state of a molecular system contains cusps
Cusp (singularity)
In the mathematical theory of singularities a cusp is a type of singular point of a curve. Cusps are local singularities in that they are not formed by self intersection points of the curve....
at the location of the nuclei, and by identifying these from the total electron density of the system, the positions are thus established. From Kato's theorem, one also obtains the nuclear charge of the nuclei, and thus the external potential is fully defined. Finally, integrating the electron density over space gives the number of electrons, and the (electronic) Hamiltonian
Molecular Hamiltonian
In atomic, molecular, and optical physics as well as in quantum chemistry, molecular Hamiltonian is the name given to the Hamiltonian representing the energy of the electrons and nuclei in a molecule...
is defined. This is valid in a non-relativistic treatment within the Born-Oppenheimer approximation
Born-Oppenheimer approximation
In quantum chemistry, the computation of the energy and wavefunction of an average-size molecule is a formidable task that is alleviated by the Born–Oppenheimer approximation, named after Max Born and J. Robert Oppenheimer. For instance the benzene molecule consists of 12 nuclei and 42...
, and assuming point-like nuclei.

