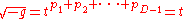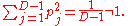Kasner metric
Encyclopedia
The Kasner metric is an exact solution
to Einstein's theory of general relativity
. It describes an anisotropic universe
without matter
(i.e., it is a vacuum solution
). It can be written in any spacetime
dimension
and has strong connections with the study of gravitational chaos
.
in
spacetime dimensions is
,
and contains
constants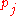 
, called the Kasner exponents. The metric describes a spacetime whose equal-time slices are spatially flat, however space is expanding or contracting at different rates in different directions, depending on the values of the 
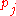. Test particles in this metric whose comoving coordinate differs by 
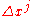are separated by a physical distance 
.
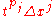The Kasner metric is an exact solution to Einstein's equations in vacuum when the Kasner exponents satisfy the following Kasner conditions,
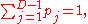
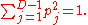
The first condition defines a plane, the Kasner plane, and the second describes a sphere
, the Kasner sphere. The solutions (choices of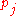
) satisfying the two conditions therefore lie on the sphere where the two intersect (sometimes confusingly also called the Kasner sphere). In 
spacetime dimensions, the space of solutions therefore lie on a 
dimensional sphere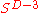 
.
Exact solutions in general relativity
In general relativity, an exact solution is a Lorentzian manifold equipped with certain tensor fields which are taken to model states of ordinary matter, such as a fluid, or classical nongravitational fields such as the electromagnetic field....
to Einstein's theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. It describes an anisotropic universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
without matter
Matter
Matter is a general term for the substance of which all physical objects consist. Typically, matter includes atoms and other particles which have mass. A common way of defining matter is as anything that has mass and occupies volume...
(i.e., it is a vacuum solution
Vacuum solution
A vacuum solution is a solution of a field equation in which the sources of the field are taken to be identically zero. That is, such field equations are written without matter interaction .-Examples:...
). It can be written in any spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
and has strong connections with the study of gravitational chaosChaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
The Metric and Kasner Conditions
The metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
in
spacetime dimensions is,and contains
constants 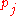, called the Kasner exponents. The metric describes a spacetime whose equal-time slices are spatially flat, however space is expanding or contracting at different rates in different directions, depending on the values of the 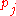. Test particles in this metric whose comoving coordinate differs by 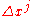are separated by a physical distance 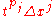.The Kasner metric is an exact solution to Einstein's equations in vacuum when the Kasner exponents satisfy the following Kasner conditions,
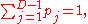
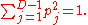
The first condition defines a plane, the Kasner plane, and the second describes a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, the Kasner sphere. The solutions (choices of
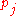) satisfying the two conditions therefore lie on the sphere where the two intersect (sometimes confusingly also called the Kasner sphere). In spacetime dimensions, the space of solutions therefore lie on a dimensional sphere 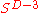.Features of the Kasner Metric
There are several noticeable and unusual features of the Kasner solution:- The volume of the spatial slices always goes like
. This is because their volume is proportional to 
, and
- where we have used the first Kasner condition. Therefore
can describe either a Big BangBig BangThe Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
or a Big CrunchBig CrunchIn physical cosmology, the Big Crunch is one possible scenario for the ultimate fate of the universe, in which the metric expansion of space eventually reverses and the universe recollapses, ultimately ending as a black hole singularity.- Overview :...
, depending on the sense of
- Isotropic expansion or contraction of spaceMetric expansion of spaceThe metric expansion of space is the increase of distance between distant parts of the universe with time. It is an intrinsic expansion—that is, it is defined by the relative separation of parts of the universe and not by motion "outward" into preexisting space...
is not allowed. If the spatial slices were expanding isotropically, then all of the Kasner exponents must be equal, and therefore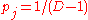
to satisfy the first Kasner condition. But then the second Kasner condition cannot be satisfied, for
- The FRW metric employed in cosmologyCosmologyCosmology is the discipline that deals with the nature of the Universe as a whole. Cosmologists seek to understand the origin, evolution, structure, and ultimate fate of the Universe at large, as well as the natural laws that keep it in order...
, by contrast, is able to expand or contract isotropically because of the presence of matter.
- With a little more work, one can show that at least one Kasner exponent is always negative (unless we are at one of the solutions with a single
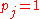, and the rest vanishing). Suppose we take the time coordinate 
to increase from zero. Then this implies that while the volume of space is increasing like 
, at least one direction (corresponding to the negative Kasner exponent) is actually contracting.
- The Kasner metric is a solution to the vacuum Einstein equations, and so the Ricci tensor always vanishes for any choice of exponents satisfying the Kasner conditions. The Riemann tensor vanishes only when a single
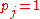and the rest vanish. This has the interesting consequence that this particular Kasner solution must be a solution of any extension of general relativity in which the field equations are built from the Riemann tensor.