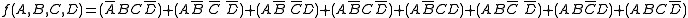Karnaugh map

Maurice Karnaugh

Maurice Karnaugh is an American physicist, famous for the Karnaugh map used in Boolean algebra.He studied mathematics and physics at City College of New York and transferred to Yale University to complete his B.Sc. , M.Sc. and Ph.D...

's 1953 refinement of Edward Veitch's 1952 Veitch diagram, is a method to simplify Boolean algebra expressions. The Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability, permitting the rapid identification and elimination of potential race condition

Race condition

A race condition or race hazard is a flaw in an electronic system or process whereby the output or result of the process is unexpectedly and critically dependent on the sequence or timing of other events...

s.

In a Karnaugh map the boolean

Boolean logic

Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...

variables are transferred (generally from a truth table

Truth table

A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...

) and ordered according to the principles of Gray code

Gray code

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....

in which only one variable changes in between adjacent squares. Once the table is generated and the output possibilities are transcribed, the data is arranged into the largest possible groups containing 2ⁿ cells (n=0,1,2,3...) and the minterm

Canonical form (Boolean algebra)

In Boolean algebra, any Boolean function can be expressed in a canonical form using the dual concepts of minterms and maxterms. Minterms are called products because they are the logical AND of a set of variables, and maxterms are called sums because they are the logical OR of a set of variables In...

is generated through the axiom laws of boolean algebra.

Example

Karnaugh maps are used to facilitate the simplification of Boolean algebra functions. The following is an unsimplified Boolean Algebra function with Boolean variables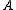

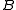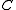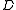, and their inverses. They can be represented in two different notations:

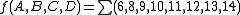Note: The values inside 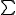are the minterms to map (i.e. rows which have output 1 in the truth table).

Truth table

Using the defined minterms, the truth table can be created: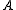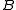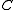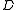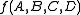

#
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

The input variables can be combined in 16 different ways, so the Karnaugh map has 16 positions, and therefore is arranged in a 4 × 4 grid.

The binary digits in the map represent the function's output for any given combination of inputs. So 0 is written in the upper leftmost corner of the map because ƒ = 0 when A = 0, B = 0, C = 0, D = 0. Similarly we mark the bottom right corner as 10 because A = 1, B = 0, C = 1, D = 0 gives ƒ = 1. Note that the values are ordered in a Gray code

Gray code

The reflected binary code, also known as Gray code after Frank Gray, is a binary numeral system where two successive values differ in only one bit. It is a non-weighted code....

, so that precisely one variable changes between any pair of adjacent cells.

After the Karnaugh map has been constructed the next task is to find the minimal terms to use in the final expression. These terms are found by encircling groups of 1s in the map. The groups must be rectangular and must have an area that is a power of two (i.e. 1, 2, 4, 8…). The rectangles should be as large as possible without containing any 0s. The optimal groupings in this map are marked by the green, red and blue lines. Note that groups may overlap. In this example, the red and green groups overlap. The red group is a 2 × 2 square, the green group is a 4 × 1 rectangle, and the overlap area is indicated in brown.

The grid is toroidally

Torus

In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...

connected, which means that the rectangular groups can wrap around edges, so

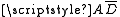is a valid term, although not part of the minimal set—this covers Minterms 8, 10, 12, and 14.

Perhaps the hardest-to-visualize wrap-around term is

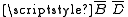which covers the four corners—this covers minterms 0, 2, 8, 10.

Solution

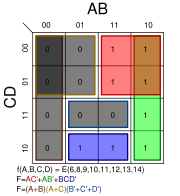
Once the Karnaugh Map has been constructed and the groups derived, the solution can be found by eliminating extra variables within groups using the axioms of boolean algebra. It can be implied that rather than eliminating the variables that change within a grouping, the minimal function can be derived by noting which variables stay the same.

For the Red grouping:

The variable 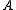maintains the same state (1) in the whole encircling, therefore it should be included in the term for the red encircling.
Variable 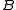does not maintain the same state (it shifts from 1 to 0), and should therefore be excluded.
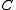does not change: it is always 0. Because 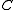is 0, it has to be negated before it is included (thus, ).
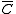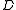changes, so it is excluded as well.

Thus the first term in the Boolean sum-of-products expression is

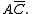
For the Green grouping we see that

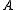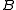maintain the same state, but

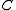and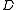

changes.

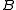is 0 and has to be negated before it can be included. Thus the second term is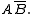

In the same way, the Blue grouping gives the term

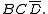
The solutions of each grouping are combined into:

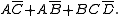
Inverse

The inverse of a function is solved in the same way by grouping the 0s instead.

The three terms to cover the inverse are all shown with grey boxes with different colored borders:

brown—
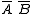
gold—
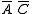
blue—

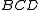
This yields the inverse:

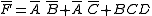
Through the use of De Morgan's laws, the product of sums can be determined:

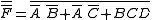
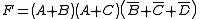
Don't cares

Karnaugh maps also allow easy minimizations of functions whose truth tables include "don't care

Don't-care (logic)

In digital logic, a don't-care term is an input-sequence to a function that the designer does not care about, usually because that input would never happen, or because differences in that input would not result in any changes to the output...

" conditions (that is, sets of inputs for which the designer doesn't care what the output is) because "don't care" conditions can be included in a circled group in an effort to make it larger. They are usually indicated on the map with a dash or X.

The example to the right is the same above example but with minterm 15 dropped and replaced as a don't care. This allows the red term to expand all the way down and, thus, removes the green term completely.

This yields the new minimum equation:

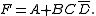
Note that the first term is just

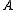not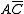

.
In this case, the don't care has dropped a term (the green); simplified another (the red); and removed the race hazard (the yellow as shown in a following section).

Also, since the inverse case no longer has to cover minterm 15, minterm 7 can be covered with

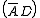rather than

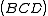with similar gains.

Elimination

Karnaugh maps are useful for detecting and eliminating race hazards. Race hazards are very easy to spot using a Karnaugh map, because a race condition may exist when moving between any pair of adjacent, but disjointed, regions circled on the map.

In the example to the right, a potential race condition exists when C is 1 and D is 0, A is 1, and B changes from 1 to 0 (moving from the blue state to the green state). For this case, tition of the output to 0) exists.
There is a second potential glitch in the same example that is more difficult to spot: when D is 0 and A and B are both 1, with C changing from 1 to 0 (moving from the blue state to the red state). In this case the glitch wraps around from the top of the map to the bottom.

Whether these glitches will actually occur depends on the physical nature of the implementation, and whether we need to worry about it depends on the application.

In this case, an additional term of

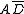would eliminate the potential race hazard, bridging between the green and blue output states or blue and red output states: this is shown as the yellow region.

The term is redundant

Logic redundancy

Logic redundancy occurs in a digital gate network containing circuitry that does not affect the static logic function. There are several reasons why logic redundancy may exist...

in terms of the static logic of the system, but such redundant, or consensus terms

Consensus theorem

In Boolean algebra, the consensus theorem is a simplification of the following terms:Proof for this theorem is: LHS = xy + x'z + yz = xy + x'z + xyz + x'yz...

, are often needed to assure race-free dynamic performance.

Similarly, an additional term of

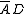must be added to the inverse to eliminate another potential race hazard. Applying De Morgan's laws creates another product of sums expression for F, but with a new factor of

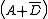2-variable map examples

The following are all the possible 2-variable, 2 × 2 Karnaugh maps. Listed with each is the minterms as a function of

and the race hazard free (see previous section) minimum equation.

External links

Quine-McCluskey algorithm implementation with a search of all solutions, by Frédéric Carpon.
Detect Overlapping Rectangles, by Herbert Glarner.
Using Karnaugh maps in practical applications, Circuit design project to control traffic lights.
K-Map Tutorial for 2,3,4 and 5 variables
Karnaugh Map Example

Software

Bmin, Qt Open Source application - Karnaugh maps and 3D Boolean n-cube visualization, Quine-McCluskey and Espresso minimization, PoS and SoP representation of functions and more.
Karma, a set of logic synthesis tools including Karnaugh maps, Quine-McCluskey minimization, teaching module and more. Logic Circuit Synthesis Labs (LogiCS) - UFRGS, Brazil.
Kmap minimizer Online Flash application, published 2009.
Boolean Function Simplification Software, freeware application for the Palm OS
Palm OS
Palm OS is a mobile operating system initially developed by Palm, Inc., for personal digital assistants in 1996. Palm OS is designed for ease of use with a touchscreen-based graphical user interface. It is provided with a suite of basic applications for personal information management...

.
GKMap, free software application at SourceForge.net
SourceForge.net
SourceForge is a web-based source code repository. It acts as a centralized location for software developers to control and manage open source software development. The website runs a version of SourceForge Enterprise Edition, forked from the last open-source version available...

.
GPA141, Java applet for solving 5-variable Karnaugh maps available only in French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...

.
Karnaugh Map Minimizer, free (but often incorrect, try with this equation : 0,1,5,8,10,13) software application at SourceForge.net
SourceForge.net
SourceForge is a web-based source code repository. It acts as a centralized location for software developers to control and manage open source software development. The website runs a version of SourceForge Enterprise Edition, forked from the last open-source version available...

.
Karnaugh Map Explorer 2.0, JavaScript application (but false with this equation : 0,2,6,8,10,11,12,13,14,15).
Simpogical, iPhone / iPad application for logic simplification.
Gorgeous Karnaugh, freeware version of Gorgeous Karnaugh K-map minimization software.
Karnaugh Minimizer, Commercial Windows application (but often incorrect, try with this equation : 0,1,5,8,10,13).
Logic Minimizer, Commercial Windows application, but can me made to run on Unix.

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

#
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

#
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0

Example

Truth table

Karnaugh map

Solution

Inverse

Don't cares

Elimination

2-variable map examples

See also

External links

#
0	0	0	0	0	0
1	0	0	0	1	0
2	0	0	1	0	0
3	0	0	1	1	0
4	0	1	0	0	0
5	0	1	0	1	0
6	0	1	1	0	1
7	0	1	1	1	0
8	1	0	0	0	1
9	1	0	0	1	1
10	1	0	1	0	1
11	1	0	1	1	1
12	1	1	0	0	1
13	1	1	0	1	1
14	1	1	1	0	1
15	1	1	1	1	0