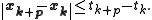Kantorovich theorem
Encyclopedia
The Kantorovich theorem is a mathematical statement on the convergence of Newton's method
. It was first stated by Leonid Kantorovich
in 1940.
Newton's method constructs a sequence of points that—with good luck—will converge to a solution x of an equation f(x) = 0 or a vector solution of a system of equation F(x) = 0. The Kantorovich theorem gives conditions on the initial point of this sequence. If those conditions are satisfied then a solution exists close to the initial point and the sequence converges to that point.
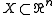 be an open subset and
be an open subset and 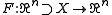 a differentiable function
a differentiable function
with a Jacobian
 that is locally Lipschitz continuous (for instance if it is twice differentiable). That is, it is assumed that for any open subset
that is locally Lipschitz continuous (for instance if it is twice differentiable). That is, it is assumed that for any open subset 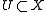 there exists a constant
there exists a constant 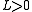 such that for any
such that for any 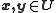
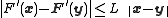
holds. The norm on the left is some operator norm that is compatible with the vector norm on the right. This inequality can be rewritten to only use the vector norm. Then for any vector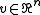 the inequality
the inequality
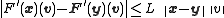
must hold.
Now choose any initial point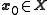 . Assume that
. Assume that 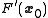 is invertible and construct the Newton step
is invertible and construct the Newton step 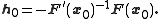
The next assumption is that not only the next point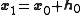 but the entire ball
but the entire ball 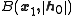 is contained inside the set X. Let
is contained inside the set X. Let 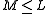 be the Lipschitz constant for the Jacobian over this ball.
be the Lipschitz constant for the Jacobian over this ball.
As a last preparation, construct recursively, as long as it is possible, the sequences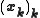 ,
, 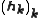 ,
,  according to
according to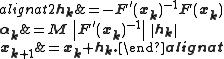
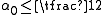 then
then
A statement that is more precise but slightly more difficult to prove uses the roots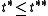 of the quadratic polynomial
of the quadratic polynomial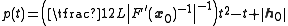 ,
,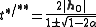
and their ratio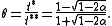
Then
Newton's method
In numerical analysis, Newton's method , named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method...
. It was first stated by Leonid Kantorovich
Leonid Kantorovich
Leonid Vitaliyevich Kantorovich was a Soviet mathematician and economist, known for his theory and development of techniques for the optimal allocation of resources...
in 1940.
Newton's method constructs a sequence of points that—with good luck—will converge to a solution x of an equation f(x) = 0 or a vector solution of a system of equation F(x) = 0. The Kantorovich theorem gives conditions on the initial point of this sequence. If those conditions are satisfied then a solution exists close to the initial point and the sequence converges to that point.
Assumptions
Let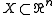 be an open subset and
be an open subset and 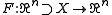 a differentiable function
a differentiable functionDifferentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
with a Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
 that is locally Lipschitz continuous (for instance if it is twice differentiable). That is, it is assumed that for any open subset
that is locally Lipschitz continuous (for instance if it is twice differentiable). That is, it is assumed that for any open subset 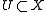 there exists a constant
there exists a constant 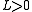 such that for any
such that for any 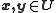
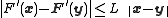
holds. The norm on the left is some operator norm that is compatible with the vector norm on the right. This inequality can be rewritten to only use the vector norm. Then for any vector
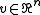 the inequality
the inequality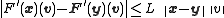
must hold.
Now choose any initial point
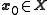 . Assume that
. Assume that 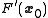 is invertible and construct the Newton step
is invertible and construct the Newton step 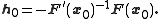
The next assumption is that not only the next point
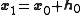 but the entire ball
but the entire ball 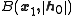 is contained inside the set X. Let
is contained inside the set X. Let 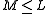 be the Lipschitz constant for the Jacobian over this ball.
be the Lipschitz constant for the Jacobian over this ball.As a last preparation, construct recursively, as long as it is possible, the sequences
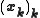 ,
, 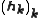 ,
,  according to
according to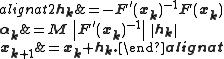
Statement
Now if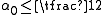 then
then
- a solution
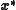 of
of 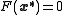 exists inside the closed ball
exists inside the closed ball 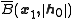 and
and - the Newton iteration starting in
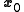 converges to
converges to 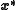 with at least linear order of convergence.
with at least linear order of convergence.
A statement that is more precise but slightly more difficult to prove uses the roots
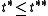 of the quadratic polynomial
of the quadratic polynomial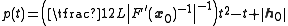 ,
,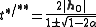
and their ratio
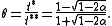
Then
- a solution
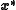 exists inside the closed ball
exists inside the closed ball 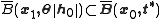
- it is unique inside the bigger ball
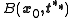
- and the convergence to the solution of F is dominated by the convergence of the Newton iteration of the quadratic polynomial p(t) towards its smallest root
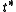 , if
, if 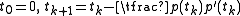 , then
, then
- The quadratic convergence is obtained from the error estimate
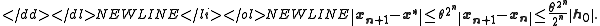
Literature
- Kantorowitsch, L. (1948): Functional analysis and applied mathematics (russ.). UMN3, 6 (28), 89–185.
- Kantorowitsch, L. W.; Akilow, G. P. (1964): Functional analysis in normed spaces.
- P. Deuflhard: Newton Methods for Nonlinear Problems. Affine Invariance and Adaptive Algorithms., Springer, Berlin 2004, ISBN 3-540-21099-7 (Springer Series in Computational Mathematics, Vol. 35)