
Jung's theorem
Encyclopedia
In geometry
, Jung's theorem is an inequality between the diameter
of a set of points in any Euclidean space
and the radius of the minimum enclosing ball of that set. It is named after Heinrich Jung, who first studied this inequality in 1901.
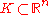
and let
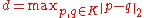
be the diameter
of K, that is, the largest Euclidean distance
between any two of its points. Jung's theorem states that there exists a closed ball with radius
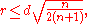
that contains K. The boundary case of equality is attained by the regular n-simplex.
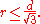
No tighter bound on r can be shown: when S is an equilateral triangle (or its three vertices), then
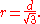
, d/2 ≤ r ≤ d. The first inequality is implied by the triangle inequality
for the center of the ball and the two diametral points, and the second inequality follows since a ball of radius d centered at any point of S will contain all of S. In a uniform metric space, that is, a space in which all distances are equal, r = d. At the other end of the spectrum, in an injective metric space
such as the Manhattan distance
in the plane, r = d/2: any two closed balls of radius d/2 centered at points of S have a nonempty intersection, therefore all such balls have a common intersection, and a radius d/2 ball centered at a point of this intersection contains all of S. Versions of Jung's theorem for various non-Euclidean geometries
are also known (see e.g. Dekster 1995, 1997).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, Jung's theorem is an inequality between the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of a set of points in any Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
and the radius of the minimum enclosing ball of that set. It is named after Heinrich Jung, who first studied this inequality in 1901.
Statement
Consider a compact set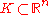
and let
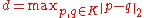
be the diameter
Diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...
of K, that is, the largest Euclidean distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between any two of its points. Jung's theorem states that there exists a closed ball with radius
Radius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
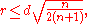
that contains K. The boundary case of equality is attained by the regular n-simplex.
Jung's theorem in the plane
Most common is the case of Jung's theorem in the plane, that is n = 2. In this case the theorem states that there exists a circle enclosing all points whose radius satisfies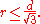
No tighter bound on r can be shown: when S is an equilateral triangle (or its three vertices), then
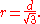
General metric spaces
For any bounded set S in any metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, d/2 ≤ r ≤ d. The first inequality is implied by the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
for the center of the ball and the two diametral points, and the second inequality follows since a ball of radius d centered at any point of S will contain all of S. In a uniform metric space, that is, a space in which all distances are equal, r = d. At the other end of the spectrum, in an injective metric space
Injective metric space
In metric geometry, an injective metric space, or equivalently a hyperconvex metric space, is a metric space with certain properties generalizing those of the real line and of L∞ distances in higher-dimensional vector spaces...
such as the Manhattan distance
Taxicab geometry
Taxicab geometry, considered by Hermann Minkowski in the 19th century, is a form of geometry in which the usual distance function or metric of Euclidean geometry is replaced by a new metric in which the distance between two points is the sum of the absolute differences of their coordinates...
in the plane, r = d/2: any two closed balls of radius d/2 centered at points of S have a nonempty intersection, therefore all such balls have a common intersection, and a radius d/2 ball centered at a point of this intersection contains all of S. Versions of Jung's theorem for various non-Euclidean geometries
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
are also known (see e.g. Dekster 1995, 1997).

