Josephson energy
Encyclopedia
In superconductivity
, the Josephson energy is the potential energy
accumulated in the Josephson junction when a supercurrent flows through it. One can think about a Josephson junction as about a non-linear inductance which accumulates (magnetic field) energy when a current passes through it. In contrast to real inductance, no magnetic field is created by a supercurrent in Josephson junction --- the accumulated energy is a Josephson energy.
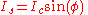
where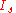
is the supercurrent flowing through the junction, 
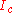is the critical current, and 
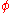is the Josephson phase
, see Josephson junction for details.
Imagine that initially at time
the junction was in the ground state 
and finally at time 
the junction has the phase 
. The work done on the junction (so the junction energy is increased by)
Here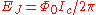
sets the characteristic scale of the Josephson energy, and
sets its dependence on the phase 
. The energy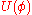 
accumulated inside the junction depends only on the current state of the junction, but not on history or velocities, i.e. it is a potential energy. Note, that 
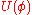has a minimum equal to zero for the ground state 
, 
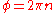is any integer.
and the supercurrent flowing through the junction is
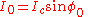
(This is the same equation as above, except now we will look at small variations in
and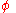 
around the values 
and 
.)
Imagine that we add little extra current (dc or ac)
through JJ, and want to see how the junction reacts. The phase across the junction changes to become 
. One can write:
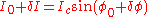
Assuming that
is small, we make a Taylor expansion in the right hand side to arrive at
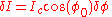
The voltage across the junction (we use the 2nd Josephson relation) is
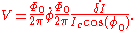
If we compare this expression with the expression for voltage across the conventional inductance
,
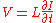we can define the so-called Josephson inductance
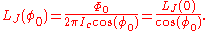
One can see that this inductance is not constant, but depends on the phase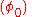
across the junction. The typical value is given by 
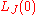and is determined only by the critical current 
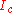. Note that, according to definition, the Josephson inductance can even become infinite or negative (if 
).
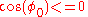One can also calcuate the change in Josephson energy
Making Taylor expansion for small
, we get
If we now compare this with the expression for increase of the inductance energy
, we again get the same expression for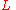 
.
Note, that although Josephson junction behaves like an inductance, there is no associated magnetic field. The corresponding energy is hidden inside the junction. The Josephson Inductance is also known as a Kinetic Inductance
- the behaviour is derived from the kinetic energy of the charge carriers, not energy in a magnetic field.
Superconductivity
Superconductivity is a phenomenon of exactly zero electrical resistance occurring in certain materials below a characteristic temperature. It was discovered by Heike Kamerlingh Onnes on April 8, 1911 in Leiden. Like ferromagnetism and atomic spectral lines, superconductivity is a quantum...
, the Josephson energy is the potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
accumulated in the Josephson junction when a supercurrent flows through it. One can think about a Josephson junction as about a non-linear inductance which accumulates (magnetic field) energy when a current passes through it. In contrast to real inductance, no magnetic field is created by a supercurrent in Josephson junction --- the accumulated energy is a Josephson energy.
Derivation
For the simplest case the current-phase relation (CPR) is given by (aka the first Josephson relation):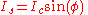where
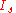is the supercurrent flowing through the junction, 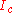is the critical current, and 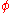is the Josephson phaseJosephson phase
In superconductivity, the Josephson phase is the difference of the phases of the quantum mechanical wave function in two superconducting electrodes forming a Josephson junction....
, see Josephson junction for details.
Imagine that initially at time
the junction was in the ground state and finally at time the junction has the phase . The work done on the junction (so the junction energy is increased by)Here
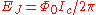
sets the characteristic scale of the Josephson energy, and
sets its dependence on the phase . The energy 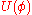accumulated inside the junction depends only on the current state of the junction, but not on history or velocities, i.e. it is a potential energy. Note, that 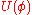has a minimum equal to zero for the ground state 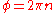, is any integer.Josephson inductance
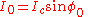
Imagine that the Josephson phase across the junction is and the supercurrent flowing through the junction is(This is the same equation as above, except now we will look at small variations in
and 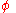around the values and .)Imagine that we add little extra current (dc or ac)
through JJ, and want to see how the junction reacts. The phase across the junction changes to become . One can write: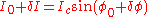Assuming that
is small, we make a Taylor expansion in the right hand side to arrive at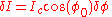The voltage across the junction (we use the 2nd Josephson relation) is
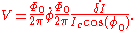
If we compare this expression with the expression for voltage across the conventional inductance
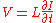,we can define the so-called Josephson inductance
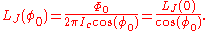
One can see that this inductance is not constant, but depends on the phase
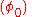across the junction. The typical value is given by 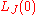and is determined only by the critical current 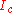. Note that, according to definition, the Josephson inductance can even become infinite or negative (if 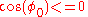).One can also calcuate the change in Josephson energy
Making Taylor expansion for small
, we getIf we now compare this with the expression for increase of the inductance energy
, we again get the same expression for 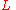.Note, that although Josephson junction behaves like an inductance, there is no associated magnetic field. The corresponding energy is hidden inside the junction. The Josephson Inductance is also known as a Kinetic Inductance
Kinetic inductance
Kinetic inductance is the manifestation of the inertial mass of mobile charge carriers in alternating electric fields as an equivalent series inductance. Kinetic inductance is observed in high carrier mobility conductors Kinetic inductance is the manifestation of the inertial mass of mobile charge...
- the behaviour is derived from the kinetic energy of the charge carriers, not energy in a magnetic field.