
Jensen's Device
Encyclopedia
Jensen's Device is a computer programming technique devised by Danish
computer scientist Jørn Jensen
, who worked with Peter Naur
at Regnecentralen
, particularly on the GIER Algol compiler, one of the earliest correct implementations of ALGOL 60
.
The following program was proposed to illustrate the technique. It computes the 100th harmonic number by the formula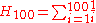 :
:
begin
integer i;
real procedure sum (i, lo, hi, term);
value lo, hi;
integer i, lo, hi;
real term;
comment term is passed by-name, and so is i;
begin
real temp;
temp := 0;
for i := lo step 1 until hi do
temp := temp + term;
sum := temp
end;
comment note the correspondence between the mathematical notation and the call to sum;
print (sum (i, 1, 100, 1/i))
end
The above exploits call by name to produce the correct answer (5.187...). It depends on the assumption that an expression passed as an actual parameter to a procedure would be re-evaluated every time the corresponding formal parameter's value was required. Thus, assignment of a value to
Denmark
Denmark is a Scandinavian country in Northern Europe. The countries of Denmark and Greenland, as well as the Faroe Islands, constitute the Kingdom of Denmark . It is the southernmost of the Nordic countries, southwest of Sweden and south of Norway, and bordered to the south by Germany. Denmark...
computer scientist Jørn Jensen
Jørn Jensen
Jørn Jensen, one of the earliest Danish programmers. Examined as a mechanical engineer and had worked with electromechanical construction. In 1958 employed at the Danish Regnecentralen, and very soon exhibited an extraordinary programming skill...
, who worked with Peter Naur
Peter Naur
Peter Naur is a Danish pioneer in computer science and Turing award winner. His last name is the N in the BNF notation , used in the description of the syntax for most programming languages...
at Regnecentralen
Regnecentralen
Regnecentralen, or RC for short, was the first Danish computer company, founded on October 12, 1955. Through the 1950s and 60s they designed a series of computers, originally for their own use, and later to be sold commercially. Descendants of these systems sold well into the 1980s...
, particularly on the GIER Algol compiler, one of the earliest correct implementations of ALGOL 60
ALGOL 60
ALGOL 60 is a member of the ALGOL family of computer programming languages. It gave rise to many other programming languages, including BCPL, B, Pascal, Simula, C, and many others. ALGOL 58 introduced code blocks and the begin and end pairs for delimiting them...
.
The following program was proposed to illustrate the technique. It computes the 100th harmonic number by the formula
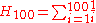 :
:begin
integer i;
real procedure sum (i, lo, hi, term);
value lo, hi;
integer i, lo, hi;
real term;
comment term is passed by-name, and so is i;
begin
real temp;
temp := 0;
for i := lo step 1 until hi do
temp := temp + term;
sum := temp
end;
comment note the correspondence between the mathematical notation and the call to sum;
print (sum (i, 1, 100, 1/i))
end
The above exploits call by name to produce the correct answer (5.187...). It depends on the assumption that an expression passed as an actual parameter to a procedure would be re-evaluated every time the corresponding formal parameter's value was required. Thus, assignment of a value to
i in the sum routine as a part of the for statement changes the value of the original i variable, and when the code of the for loop requires the value of term, the expression 1/i is evaluated and with the new value of i. If the last parameter to sum had been passed by value, and assuming the initial value of i were 1, the result would have been 100 × 1/1 = 100, though actually, it is not initialised.
So, the first parameter to sum,
representing the "bound" variable of the summation,
must also be passed by name, otherwise it would not be possible
to compute the values to be added.
On the other hand, the global variable does not have to use the same identifier,
in this case i, as the formal parameter.
Usage
The Sum function can be employed for arbitrary functions merely by employing the appropriate expressions. If a sum of integers were desired the expression would be just sum(i,1,100,i);, if a sum of squares of integers, then sum(i,1,100,i*i);, and so on. A slight variation would be suitable for initiating a numerical integration of an expression by a method very similar to that of sum. In the absence of this pass-by-name facility, it would be necessary to define functions embodying those expressions to be passed according to the protocols of the computer language, or to create a compendium function along with some arrangement to select the desired expression for each usage.
Because every mention of term within the procedure re-evaluates the original expression, making a local copy of the value of term as appropriate may be worthwhile, as when the procedure might compute the product of the terms as well as their sum.

