In mathematics, the fourth Janko group J₄ is the sporadic

Sporadic group

In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...

 finite simple group of order 2²¹ · 3³ · 5 · 7 · 11³ · 23 · 29 · 31 · 37 · 43 = 86775571046077562880 whose existence was suggested by Zvonimir Janko

Zvonimir Janko

Zvonimir Janko is a Croatian mathematician who is the eponym of the Janko groups, sporadic simple groups in group theory.Janko was born in Bjelovar, Croatia. He studied at the University of Zagreb where he received Ph.D. in 1960. He then taught physics at a high school in Široki Brijeg in Bosnia...

 (1976). Its existence and uniqueness was shown by Simon P. Norton

Simon P. Norton

Simon Phillips Norton is a mathematician in Cambridge, England, who works on finite simple groups. He constructed the Harada–Norton group, and in 1979 together with John Conway proved there is a connection between the Monster group and the j-function in number theory. They dubbed this monstrous...

 and others in 1980. Janko found it by studying groups with an involution centralizer of the form 2^{1 + 12}.3.(M₂₂:2). It has a modular representation of dimension 112 over the finite field of two elements and is the stabilizer of a certain 4995 dimensional subspace of the exterior square, a fact which Norton used to construct it, and which is the easiest way to deal with it computationally. The Schur multiplier and the outer automorphism group are both trivial. has given a proof of existence and uniqueness that does not rely on computer calculations.

J₄ is one of the 6 sporadic simple groups called the pariahs

Pariah group

In mathematical group theory, the term pariah was introduced by to refer to the six sporadic simple groups that are not subquotients of the monster simple group.These groups are:*Three of the Janko groups: J1, J3, and J4.*The Lyons group...

, because they are not found within the Monster group

Monster group

In the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...

. The order of the monster group is not divisible by 37 or 43.

Presentation

It has a presentation in terms of three generators a, b, and c as

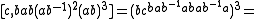
Maximal subgroups

showed that J₄ has 13 conjugacy classes of maximal subgroups.

• 2¹¹:M₂₄ - containing Sylow 2-subgroups and Sylow 3-subgroups; also containing 2¹¹:(M₂₂:2), centralizer of involution of class 2B
• 2¹⁺¹².3.(M₂₂:2) - centralizer of involution of class 2A - containing Sylow 2-subgroups and Sylow 3-subgroups
• 2¹⁰:PSL(5,2)
• 2³⁺¹².(S₅ × PSL(3,2)) - containing Sylow 2-subgroups
• U₃(11):2
• M₂₂:2
• 11¹⁺²:(5 × GL(2,3)) - normalizer of Sylow 11-subgroup
• PSL(2,32):5
• PGL(2,23)
• U₃(3) - containing Sylow 3-subgroups
• 29:28 = F₈₁₂
• 43:14 = F₆₀₂
• 37:12 = F₄₄₄

A Sylow 3-subgroup is a Heisenberg group: order 27, non-abelian, all non-trivial elements of order 3