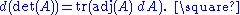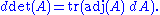Jacobi's formula
Encyclopedia
In matrix calculus
, Jacobi's formula expresses the derivative
of the determinant
of a matrix A in terms of the adjugate of A and the derivative of A. If A is a differentiable map from the real numbers to n × n matrices,

Equivalently, if dA stands for the differential of A, the formula is
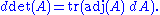
It is named after the mathematician C.G.J. Jacobi.
Lemma. Let A and B be a pair of square matrices of the same dimension n. Then
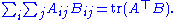
Proof. The product AB of the pair of matrices has components
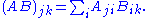
Replacing the matrix A by its transpose
AT is equivalent to permuting the indices of its components:
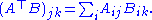
The result follows by taking the trace of both sides:
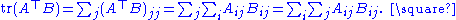
Theorem. (Jacobi's formula) For any differentiable map A from the real numbers to n × n matrices,
Proof. Laplace's formula
for the determinant of a matrix A can be stated as
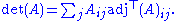
Notice that the summation is performed over some arbitrary row i of the matrix.
The determinant of A can be considered to be a function of the elements of A:
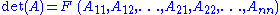
so that, by the chain rule
, its differential is
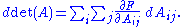
This summation is performed over all n×n elements of the matrix.
To find ∂F/∂Aij consider that on the right hand side of Laplace's formula, the index i can be chosen at will. (In order to optimize calculations: Any other choice would eventually yield the same result, but it could be much harder). In particular, it can be chosen to match the first index of ∂ / ∂Aij:
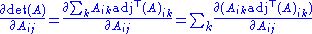
Thus, by the product rule,

Now, if an element of a matrix Aij and a cofactor
adjT(A)ik of element Aik lie on the same row (or column), then the cofactor will not be a function of Aij, because the cofactor of Aik is expressed in terms of elements not in its own row (nor column). Thus,
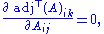
so
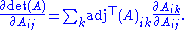
All the elements of A are independent of each other, i.e.
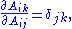
where δ is the Kronecker delta, so

Therefore,
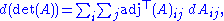
and applying the Lemma yields
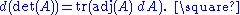
Matrix calculus
In mathematics, matrix calculus is a specialized notation for doing multivariable calculus, especially over spaces of matrices, where it defines the matrix derivative. This notation was to describe systems of differential equations, and taking derivatives of matrix-valued functions with respect...
, Jacobi's formula expresses the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of the determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
of a matrix A in terms of the adjugate of A and the derivative of A. If A is a differentiable map from the real numbers to n × n matrices,

Equivalently, if dA stands for the differential of A, the formula is
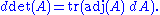
It is named after the mathematician C.G.J. Jacobi.
Derivation
We first prove a preliminary lemma:Lemma. Let A and B be a pair of square matrices of the same dimension n. Then
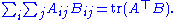
Proof. The product AB of the pair of matrices has components
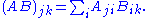
Replacing the matrix A by its transpose
Transpose
In linear algebra, the transpose of a matrix A is another matrix AT created by any one of the following equivalent actions:...
AT is equivalent to permuting the indices of its components:
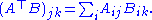
The result follows by taking the trace of both sides:
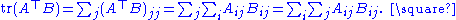
Theorem. (Jacobi's formula) For any differentiable map A from the real numbers to n × n matrices,
Proof. Laplace's formula
Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression for the determinant |B| of...
for the determinant of a matrix A can be stated as
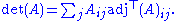
Notice that the summation is performed over some arbitrary row i of the matrix.
The determinant of A can be considered to be a function of the elements of A:
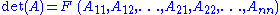
so that, by the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, its differential is
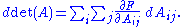
This summation is performed over all n×n elements of the matrix.
To find ∂F/∂Aij consider that on the right hand side of Laplace's formula, the index i can be chosen at will. (In order to optimize calculations: Any other choice would eventually yield the same result, but it could be much harder). In particular, it can be chosen to match the first index of ∂ / ∂Aij:
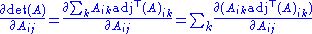
Thus, by the product rule,

Now, if an element of a matrix Aij and a cofactor
Minor (linear algebra)
In linear algebra, a minor of a matrix A is the determinant of some smaller square matrix, cut down from A by removing one or more of its rows or columns...
adjT(A)ik of element Aik lie on the same row (or column), then the cofactor will not be a function of Aij, because the cofactor of Aik is expressed in terms of elements not in its own row (nor column). Thus,
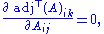
so
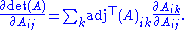
All the elements of A are independent of each other, i.e.
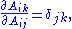
where δ is the Kronecker delta, so

Therefore,
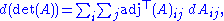
and applying the Lemma yields