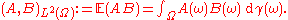Ito isometry
Encyclopedia
In mathematics
, the Itō isometry, named after Kiyoshi Itō
, is a crucial fact about Itō stochastic integrals
. One of its main applications is to enable the computation of variance
s for stochastic processes.
Let denote the canonical real-valued Wiener process
denote the canonical real-valued Wiener process
defined up to time , and let
, and let  be a stochastic process that is adapted
be a stochastic process that is adapted
to the natural filtration
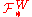 of the Wiener process. Then
of the Wiener process. Then
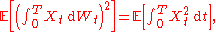
where denotes expectation
denotes expectation
with respect to classical Wiener measure . In other words, the Itō stochastic integral, as a function, is an isometry
. In other words, the Itō stochastic integral, as a function, is an isometry
of normed vector space
s with respect to the norms induced by the inner products
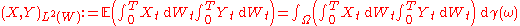
and
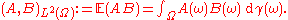
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Itō isometry, named after Kiyoshi Itō
Kiyoshi Ito
was a Japanese mathematician whose work is now called Itō calculus. The basic concept of this calculus is the Itō integral, and among the most important results is Itō's lemma. The Itō calculus facilitates mathematical understanding of random events...
, is a crucial fact about Itō stochastic integrals
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
. One of its main applications is to enable the computation of variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
s for stochastic processes.
Let
 denote the canonical real-valued Wiener process
denote the canonical real-valued Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
defined up to time
 , and let
, and let  be a stochastic process that is adapted
be a stochastic process that is adaptedAdapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
to the natural filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
 of the Wiener process. Then
of the Wiener process. Then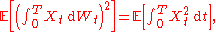
where
 denotes expectation
denotes expectationExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
with respect to classical Wiener measure
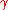 . In other words, the Itō stochastic integral, as a function, is an isometry
. In other words, the Itō stochastic integral, as a function, is an isometryIsometry
In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
s with respect to the norms induced by the inner products
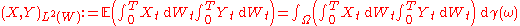
and