An isothetic polygon is a polygon

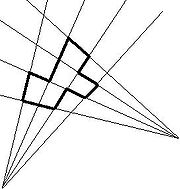
Polygon

In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...

 whose alternate sides belong to two parametric families of straight lines which are pencils

Pencil (mathematics)

A pencil in projective geometry is a family of geometric objects with a common property, for example the set of lines that pass through a given point in a projective plane....

 of lines with centers at two points (possibly in the infinity

Infinity

Infinity is a concept in many fields, most predominantly mathematics and physics, that refers to a quantity without bound or end. People have developed various ideas throughout history about the nature of infinity...

). The most well-known example of isothetic polygons are rectilinear polygon

Rectilinear polygon

A rectilinear polygon is a polygon all of whose edges meet at right angles. Thus the interior angle at each vertex is either 90° or 270°. Rectilinear polygons are a special case of isothetic polygons....

s, and the former term is commonly used as a synonym

Synonym

Synonyms are different words with almost identical or similar meanings. Words that are synonyms are said to be synonymous, and the state of being a synonym is called synonymy. The word comes from Ancient Greek syn and onoma . The words car and automobile are synonyms...

 for the latter one.

Etymology and history

The term is produced from Greek roots: iso- for "equal, same, similar" and thetos (position, placement), i,e., the term is supposed to mean "polygon with similarly placed sides".

The term was suggested during the early years of the computational geometry

Computational geometry

Computational geometry is a branch of computer science devoted to the study of algorithms which can be stated in terms of geometry. Some purely geometrical problems arise out of the study of computational geometric algorithms, and such problems are also considered to be part of computational...

. Much emphasis was placed on the development of efficient algorithms

Computational Complexity

Computational Complexity may refer to:*Computational complexity theory*Computational Complexity...

 for operations with orthogonal polygons, since the latter ones had an important application: representation of shapes in integrated circuit

Integrated circuit

An integrated circuit or monolithic integrated circuit is an electronic circuit manufactured by the patterned diffusion of trace elements into the surface of a thin substrate of semiconductor material...

 mask layout

Integrated circuit layout

Integrated circuit layout, also known IC layout, IC mask layout, or mask design, is the representation of an integrated circuit in terms of planar geometric shapes which correspond to the patterns of metal, oxide, or semiconductor layers that make up the components of the integrated circuit.When...

s due to their simplicity for design and manufacturing. It was observed that the efficiency of many geometric algorithms for orthogonal polygons does not really depend on the fact that their sides meet at right angles, but rather on the fact that their sides are naturally split into two alternating sets (of vertical and horizontal segments).

----

----

Sets of isothetic polygons

In many applications of computational geometry, when a problem is stated for a set of rectilinear polygons, it is very often implicitly assumed that these polygons have the same alignment (in fact, aligned to the same orthogonal coordinate axes), and hence the term "isothetic polygons" would be less ambiguous. In the context of digital geometry

Digital geometry

Digital geometry deals with discrete sets considered to be digitized models or images of objects of the 2D or 3D Euclidean space.Simply put, digitizing is replacing an object by a discrete set of its points...

, isothetic polygons are practically axis-parallel and have integer coordinates of their vertices.