Interaction information
Encyclopedia
The interaction information (McGill 1954) or co-information (Bell 2003) is one of several generalizations of the mutual information
, and expresses the amount information (redundancy or synergy) bound up in a set of variables, beyond that which is present in any subset of those variables. Unlike the mutual information, the interaction information can be either positive or negative. This confusing property has likely retarded its wider adoption as an information measure in machine learning and cognitive science.
 , the interaction information
, the interaction information  is given by
is given by

where, for example, is the mutual information between variables
is the mutual information between variables  and
and  , and
, and  is the conditional mutual information
is the conditional mutual information
between variables and
and  given
given  . Formally,
. Formally,

For the three-variable case, the interaction information is the difference between the information shared by
is the difference between the information shared by  when
when  has been fixed and when
has been fixed and when  has not been fixed. (See also Fano's 1961 textbook.) Interaction information measures the influence of a variable
has not been fixed. (See also Fano's 1961 textbook.) Interaction information measures the influence of a variable  on the amount of information shared between
on the amount of information shared between  . Because the term
. Because the term  can be zero — for example, when the
can be zero — for example, when the
dependency between is due entirely to the influence of a common cause
is due entirely to the influence of a common cause  , the interaction information can be negative as well as positive. Negative interaction information indicates that variable
, the interaction information can be negative as well as positive. Negative interaction information indicates that variable  inhibits (i.e., accounts for or explains some of) the correlation between
inhibits (i.e., accounts for or explains some of) the correlation between  , whereas positive interaction information indicates that variable
, whereas positive interaction information indicates that variable  facilitates or enhances the correlation between
facilitates or enhances the correlation between  .
.
Interaction information is bounded. In the three variable case, it is bounded by

 . The result is negative interaction information
. The result is negative interaction information  .
.
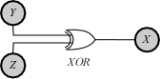
 The case of positive interaction information seems a bit less natural. A prototypical example of positive
The case of positive interaction information seems a bit less natural. A prototypical example of positive  has
has  as the output of an XOR gate to which
as the output of an XOR gate to which  and
and  are the independent random inputs. In this case
are the independent random inputs. In this case  will be zero, but
will be zero, but  will be positive (1 bit
will be positive (1 bit
) since once output is known, the value on input
is known, the value on input  completely determines the value on input
completely determines the value on input  . Since
. Since  , the result is positive interaction information
, the result is positive interaction information  . It may seem that this example relies on a peculiar ordering of
. It may seem that this example relies on a peculiar ordering of  to obtain the positive interaction, but the symmetry of the definition for
to obtain the positive interaction, but the symmetry of the definition for  indicates that the same positive interaction information results regardless of which variable we consider as the interloper or conditioning variable. For example, input
indicates that the same positive interaction information results regardless of which variable we consider as the interloper or conditioning variable. For example, input  and output
and output  are also independent until input
are also independent until input  is fixed, at which time they are totally dependent (obviously), and we have the same positive interaction information as before,
is fixed, at which time they are totally dependent (obviously), and we have the same positive interaction information as before,  .
.
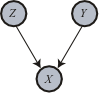 This situation is an instance where fixing the common effect
This situation is an instance where fixing the common effect  of causes
of causes  and
and  induces a dependency among the causes that did not formerly exist. This behavior is colloquially referred to as explaining away and is thoroughly discussed in the Bayesian Network
induces a dependency among the causes that did not formerly exist. This behavior is colloquially referred to as explaining away and is thoroughly discussed in the Bayesian Network
literature (e.g., Pearl 1988). Pearl's example is auto diagnostics: A car's engine can fail to start due either to a dead battery
due either to a dead battery  or due to a blocked fuel pump
or due to a blocked fuel pump  . Ordinarily, we assume that battery death and fuel pump blockage are independent events, because of the essential modularity of such automotive systems. Thus, in the absence of other information, knowing whether or not the battery is dead gives us no information about whether or not the fuel pump is blocked. However, if we happen to know that the car fails to start (i.e., we fix common effect
. Ordinarily, we assume that battery death and fuel pump blockage are independent events, because of the essential modularity of such automotive systems. Thus, in the absence of other information, knowing whether or not the battery is dead gives us no information about whether or not the fuel pump is blocked. However, if we happen to know that the car fails to start (i.e., we fix common effect  ), this information induces a dependency between the two causes battery death and fuel blockage. Thus, knowing that the car fails to start, if an inspection shows the battery to be in good health, we can conclude that the fuel pump must be blocked.
), this information induces a dependency between the two causes battery death and fuel blockage. Thus, knowing that the car fails to start, if an inspection shows the battery to be in good health, we can conclude that the fuel pump must be blocked.
Battery death and fuel blockage are thus dependent, conditional on their common effect car starting. What the foregoing discussion indicates is that the obvious directionality in the common-effect graph belies a deep informational symmetry: If conditioning on a common effect
increases the dependency between its two parent causes, then conditioning on one of the causes must create the same increase in dependency between the second cause and the common effect. In Pearl's automotive example, if conditioning on car starts induces bits of dependency between the two causes battery dead and fuel blocked, then conditioning on
bits of dependency between the two causes battery dead and fuel blocked, then conditioning on
fuel blocked must induce bits of dependency between battery dead and car starts. This may seem odd because battery dead and car starts are already governed by the implication battery dead
bits of dependency between battery dead and car starts. This may seem odd because battery dead and car starts are already governed by the implication battery dead  car doesn't start. However, these variables are still not totally correlated because the converse is not true. Conditioning on fuel blocked removes the major alternate cause of failure to start, and strengthens the converse relation and therefore the association between battery dead and car starts. A paper by Tsujishita (1995) focuses in greater depth on the third-order mutual information.
car doesn't start. However, these variables are still not totally correlated because the converse is not true. Conditioning on fuel blocked removes the major alternate cause of failure to start, and strengthens the converse relation and therefore the association between battery dead and car starts. A paper by Tsujishita (1995) focuses in greater depth on the third-order mutual information.
 -dimensional interaction information. For example, the four-dimensional interaction information can be defined as
-dimensional interaction information. For example, the four-dimensional interaction information can be defined as

or, equivalently,

 in terms of the marginal entropies is given by Jakulin & Bratko (2003).
in terms of the marginal entropies is given by Jakulin & Bratko (2003).

which is an alternating (inclusion-exclusion) sum over all subsets , where
, where  . Note
. Note
that this is the information-theoretic analog to the Kirkwood approximation
.
 . Agglomerate these variables as follows:
. Agglomerate these variables as follows:

Because the 's overlap each other (are redundant) on the three binary variables
's overlap each other (are redundant) on the three binary variables  , we would expect the interaction information
, we would expect the interaction information  to equal
to equal  bits, which it does. However, consider
bits, which it does. However, consider
now the agglomerated variables

These are the same variables as before with the addition of . Because the
. Because the  's now overlap each other (are redundant) on only one binary variable
's now overlap each other (are redundant) on only one binary variable  , we would expect the interaction information
, we would expect the interaction information  to equal
to equal  bit. However,
bit. However,  in this case is actually equal to
in this case is actually equal to  bit,
bit,
indicating a synergy rather than a redundancy. This is correct in the sense that

but it remains difficult to interpret.
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
, and expresses the amount information (redundancy or synergy) bound up in a set of variables, beyond that which is present in any subset of those variables. Unlike the mutual information, the interaction information can be either positive or negative. This confusing property has likely retarded its wider adoption as an information measure in machine learning and cognitive science.
The Three-Variable Case
For three variables , the interaction information
, the interaction information  is given by
is given by
where, for example,
 is the mutual information between variables
is the mutual information between variables  and
and  , and
, and  is the conditional mutual information
is the conditional mutual informationConditional mutual information
In probability theory, and in particular, information theory, the conditional mutual information is, in its most basic form, the expected value of the mutual information of two random variables given the value of a third.-Definition:...
between variables
 and
and  given
given  . Formally,
. Formally,
For the three-variable case, the interaction information
 is the difference between the information shared by
is the difference between the information shared by  when
when  has been fixed and when
has been fixed and when  has not been fixed. (See also Fano's 1961 textbook.) Interaction information measures the influence of a variable
has not been fixed. (See also Fano's 1961 textbook.) Interaction information measures the influence of a variable  on the amount of information shared between
on the amount of information shared between  . Because the term
. Because the term  can be zero — for example, when the
can be zero — for example, when thedependency between
 is due entirely to the influence of a common cause
is due entirely to the influence of a common cause  , the interaction information can be negative as well as positive. Negative interaction information indicates that variable
, the interaction information can be negative as well as positive. Negative interaction information indicates that variable  inhibits (i.e., accounts for or explains some of) the correlation between
inhibits (i.e., accounts for or explains some of) the correlation between  , whereas positive interaction information indicates that variable
, whereas positive interaction information indicates that variable  facilitates or enhances the correlation between
facilitates or enhances the correlation between  .
.Interaction information is bounded. In the three variable case, it is bounded by

Example of Negative Interaction Information
Negative interaction information seems much more natural than positive interaction information in the sense that such explanatory effects are typical of common-cause structures. For example, clouds cause rain and also block the sun; therefore, the correlation between rain and darkness is partly accounted for by the presence of clouds, . The result is negative interaction information
. The result is negative interaction information  .
.Example of Positive Interaction Information
 The case of positive interaction information seems a bit less natural. A prototypical example of positive
The case of positive interaction information seems a bit less natural. A prototypical example of positive  has
has  as the output of an XOR gate to which
as the output of an XOR gate to which  and
and  are the independent random inputs. In this case
are the independent random inputs. In this case  will be zero, but
will be zero, but  will be positive (1 bit
will be positive (1 bitBit
A bit is the basic unit of information in computing and telecommunications; it is the amount of information stored by a digital device or other physical system that exists in one of two possible distinct states...
) since once output
 is known, the value on input
is known, the value on input  completely determines the value on input
completely determines the value on input  . Since
. Since  , the result is positive interaction information
, the result is positive interaction information  . It may seem that this example relies on a peculiar ordering of
. It may seem that this example relies on a peculiar ordering of  to obtain the positive interaction, but the symmetry of the definition for
to obtain the positive interaction, but the symmetry of the definition for  indicates that the same positive interaction information results regardless of which variable we consider as the interloper or conditioning variable. For example, input
indicates that the same positive interaction information results regardless of which variable we consider as the interloper or conditioning variable. For example, input  and output
and output  are also independent until input
are also independent until input  is fixed, at which time they are totally dependent (obviously), and we have the same positive interaction information as before,
is fixed, at which time they are totally dependent (obviously), and we have the same positive interaction information as before,  .
. This situation is an instance where fixing the common effect
This situation is an instance where fixing the common effect  of causes
of causes  and
and  induces a dependency among the causes that did not formerly exist. This behavior is colloquially referred to as explaining away and is thoroughly discussed in the Bayesian Network
induces a dependency among the causes that did not formerly exist. This behavior is colloquially referred to as explaining away and is thoroughly discussed in the Bayesian NetworkBayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
literature (e.g., Pearl 1988). Pearl's example is auto diagnostics: A car's engine can fail to start
 due either to a dead battery
due either to a dead battery  or due to a blocked fuel pump
or due to a blocked fuel pump  . Ordinarily, we assume that battery death and fuel pump blockage are independent events, because of the essential modularity of such automotive systems. Thus, in the absence of other information, knowing whether or not the battery is dead gives us no information about whether or not the fuel pump is blocked. However, if we happen to know that the car fails to start (i.e., we fix common effect
. Ordinarily, we assume that battery death and fuel pump blockage are independent events, because of the essential modularity of such automotive systems. Thus, in the absence of other information, knowing whether or not the battery is dead gives us no information about whether or not the fuel pump is blocked. However, if we happen to know that the car fails to start (i.e., we fix common effect  ), this information induces a dependency between the two causes battery death and fuel blockage. Thus, knowing that the car fails to start, if an inspection shows the battery to be in good health, we can conclude that the fuel pump must be blocked.
), this information induces a dependency between the two causes battery death and fuel blockage. Thus, knowing that the car fails to start, if an inspection shows the battery to be in good health, we can conclude that the fuel pump must be blocked.Battery death and fuel blockage are thus dependent, conditional on their common effect car starting. What the foregoing discussion indicates is that the obvious directionality in the common-effect graph belies a deep informational symmetry: If conditioning on a common effect
increases the dependency between its two parent causes, then conditioning on one of the causes must create the same increase in dependency between the second cause and the common effect. In Pearl's automotive example, if conditioning on car starts induces
 bits of dependency between the two causes battery dead and fuel blocked, then conditioning on
bits of dependency between the two causes battery dead and fuel blocked, then conditioning onfuel blocked must induce
 bits of dependency between battery dead and car starts. This may seem odd because battery dead and car starts are already governed by the implication battery dead
bits of dependency between battery dead and car starts. This may seem odd because battery dead and car starts are already governed by the implication battery dead  car doesn't start. However, these variables are still not totally correlated because the converse is not true. Conditioning on fuel blocked removes the major alternate cause of failure to start, and strengthens the converse relation and therefore the association between battery dead and car starts. A paper by Tsujishita (1995) focuses in greater depth on the third-order mutual information.
car doesn't start. However, these variables are still not totally correlated because the converse is not true. Conditioning on fuel blocked removes the major alternate cause of failure to start, and strengthens the converse relation and therefore the association between battery dead and car starts. A paper by Tsujishita (1995) focuses in greater depth on the third-order mutual information.The Four-Variable Case
One can recursively define the n-dimensional interaction information in terms of the -dimensional interaction information. For example, the four-dimensional interaction information can be defined as
-dimensional interaction information. For example, the four-dimensional interaction information can be defined as
or, equivalently,

The n-Variable Case
It is possible to extend all of these results to an arbitrary number of dimensions. The general expression for interaction information on variable set in terms of the marginal entropies is given by Jakulin & Bratko (2003).
in terms of the marginal entropies is given by Jakulin & Bratko (2003).
which is an alternating (inclusion-exclusion) sum over all subsets
 , where
, where  . Note
. Notethat this is the information-theoretic analog to the Kirkwood approximation
Kirkwood approximation
The Kirkwood superposition approximation was introduced by Matsuda as a means of representing a discrete probability distribution. The name apparently refers to a 1942 paper by John G. Kirkwood...
.
Difficulties Interpreting Interaction Information
The possible negativity of interaction information can be the source of some confusion (Bell 2003). As an example of this confusion, consider a set of eight independent binary variables . Agglomerate these variables as follows:
. Agglomerate these variables as follows:
Because the
 's overlap each other (are redundant) on the three binary variables
's overlap each other (are redundant) on the three binary variables  , we would expect the interaction information
, we would expect the interaction information  to equal
to equal  bits, which it does. However, consider
bits, which it does. However, considernow the agglomerated variables

These are the same variables as before with the addition of
 . Because the
. Because the  's now overlap each other (are redundant) on only one binary variable
's now overlap each other (are redundant) on only one binary variable  , we would expect the interaction information
, we would expect the interaction information  to equal
to equal  bit. However,
bit. However,  in this case is actually equal to
in this case is actually equal to  bit,
bit,indicating a synergy rather than a redundancy. This is correct in the sense that

but it remains difficult to interpret.
Uses of Interaction Information
- Jakulin and Bratko (2003b) provide a machine learning algorithm which uses interaction information.
- Killian, Kravitz and Gilson (2007) use mutual information expansion to extract entropy estimates from molecular simulations.
- Moore et al. (2006), Chanda P, Zhang A, Brazeau D, Sucheston L, Freudenheim JL, Ambrosone C, Ramanathan M. (2007) and Chanda P, Sucheston L, Zhang A, Brazeau D, Freudenheim JL, Ambrosone C, Ramanathan M. (2008) demonstrate the use of interaction information for analyzing gene-gene and gene-environmental interactions associated with complex diseases.

