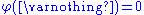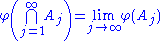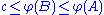Inner measure
Encyclopedia
In mathematics
, in particular in measure theory, an inner measure is a function
on the set of all subsets of members of a given σ-algebra with values in the extended real numbers satisfying some technical conditions. Intuitively, the inner measure of a set is a lower bound of the size of that set.
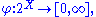
defined on all subsets of a set X, that satisfies the following conditions:
on Σ.
Then the inner measure μ* induced by μ is defined by
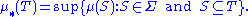
Essentially μ* gives a lower bound of the size of any set by insuring it is at least as big as the μ-measure of any of its Σ-measurable subsets. Even though the set function μ* is usually not a measure, μ* shares the following properties with measures:
s to extend a measure to a larger σ-algebra. If μ is a measure defined on σ-algebra Σ over X and μ* and μ* are corresponding induced outer and inner measures, then the sets T ∈ 2X such that μ*(T) = μ*(T) form a σ-algebra with
with 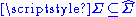 . The set function μ̂ defined by
. The set function μ̂ defined by
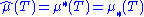 ,
,
for all T ∈ is a measure on
is a measure on  known as the completion of μ.
known as the completion of μ.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in particular in measure theory, an inner measure is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on the set of all subsets of members of a given σ-algebra with values in the extended real numbers satisfying some technical conditions. Intuitively, the inner measure of a set is a lower bound of the size of that set.
Definition
An inner measure is a function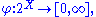
defined on all subsets of a set X, that satisfies the following conditions:
- Null empty set: The empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
has zero inner measure (see also: measure zero).
- Superadditive: For any disjoint sets A and B,
- Limits of decreasing towers: For any sequence {Aj} of sets such that
 for each j and
for each j and 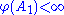
- Infinity must be approached: If
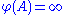 for a set A then for every positive number c, there exists a B which is a subset of A such that,
for a set A then for every positive number c, there exists a B which is a subset of A such that,
The inner measure induced by a measure
Let Σ be a σ-algebra over a set X and μ be a measureMeasure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on Σ.
Then the inner measure μ* induced by μ is defined by
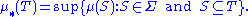
Essentially μ* gives a lower bound of the size of any set by insuring it is at least as big as the μ-measure of any of its Σ-measurable subsets. Even though the set function μ* is usually not a measure, μ* shares the following properties with measures:
-
- μ*(∅)=0,
- μ* is non-negative,
- If E ⊆ F then μ*(E) ≤ μ*(F).
Measure completion
Induced inner measures are often used in combination with outer measureOuter measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
s to extend a measure to a larger σ-algebra. If μ is a measure defined on σ-algebra Σ over X and μ* and μ* are corresponding induced outer and inner measures, then the sets T ∈ 2X such that μ*(T) = μ*(T) form a σ-algebra
 with
with 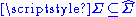 . The set function μ̂ defined by
. The set function μ̂ defined by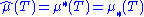 ,
,for all T ∈
 is a measure on
is a measure on  known as the completion of μ.
known as the completion of μ.