
Hrushovski construction
Encyclopedia
In model theory
, a branch of mathematical logic
, the Hrushovski construction generalizes the Fraïssé limit
by working with a notion of strong substructure rather than
rather than  . It can be thought of as a kind of "model-theoretic forcing", where a (usually) stable structure is created, called the generic. The specifics of
. It can be thought of as a kind of "model-theoretic forcing", where a (usually) stable structure is created, called the generic. The specifics of  determine various properties of the generic, with its geometric properties being of particular interest. It was initially used by Ehud Hrushovski
determine various properties of the generic, with its geometric properties being of particular interest. It was initially used by Ehud Hrushovski
to generate a stable structure with an "exotic" geometry, thereby refuting Zil'ber's Conjecture.
substructures. We want to strengthen the notion of substructure; let
 be a relation on pairs from C satisfying:
be a relation on pairs from C satisfying:
An embedding is strong if
is strong if 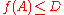 .
.
We also want the pair (C, ) to satisfy the amalgamation property: if
) to satisfy the amalgamation property: if  then there is a
then there is a 
so that each embeds strongly into
embeds strongly into  with the same image for
with the same image for
 .
.
For infinite , and
, and  , we say
, we say  iff
iff  for
for
 ,
,  . For any
. For any  , the
, the
closure of (in
(in  ),
), 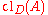 is the smallest superset of
is the smallest superset of 
satisfying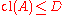 .
.
Definition A countable structure is a (C,
is a (C,  )-generic if:
)-generic if:
Theorem If (C, ) has the amalgamation property, then there is a unique (C,
) has the amalgamation property, then there is a unique (C,  )-generic.
)-generic.
The existence proof proceeds in imitation of the existence proof for
Fraïssé limits. The uniqueness proof comes from an easy back and forth
argument.
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
, a branch of mathematical logic
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the Hrushovski construction generalizes the Fraïssé limit
Age (model theory)
In model theory, the age of a structure A is the class of all finitely generated structures which are embeddable in A . This concept is central in the construction of a Fraïssé limit....
by working with a notion of strong substructure
 rather than
rather than  . It can be thought of as a kind of "model-theoretic forcing", where a (usually) stable structure is created, called the generic. The specifics of
. It can be thought of as a kind of "model-theoretic forcing", where a (usually) stable structure is created, called the generic. The specifics of  determine various properties of the generic, with its geometric properties being of particular interest. It was initially used by Ehud Hrushovski
determine various properties of the generic, with its geometric properties being of particular interest. It was initially used by Ehud HrushovskiEhud Hrushovski
Ehud Hrushovski is a mathematical logician. He is a Professor of Mathematics at the Hebrew University of Jerusalem.His father, Benjamin Harshav, is Emeritus Professor in Yale University and Tel Aviv University to Comparative Literature and a poet....
to generate a stable structure with an "exotic" geometry, thereby refuting Zil'ber's Conjecture.
Three conjectures
The initial applications of the Hrushovski construction refuted two conjectures and answered a third question in the negative. Specifically, we have:- Lachlan's Conjecture Any stable
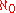 -categorical theory is totally transcendental.
-categorical theory is totally transcendental.
- Zil'ber's Conjecture Any uncountably categorical theory is either locally modular or interprets an algebraically closed field.
- Cherlin's Question Is there a maximal (with respect to expansions) strongly minimal set?
The construction
Let L be a finite relational language. Fix C a class of finite L-structures which are closed under isomorphisms andsubstructures. We want to strengthen the notion of substructure; let
 be a relation on pairs from C satisfying:
be a relation on pairs from C satisfying:-
 implies
implies  .
. -
 and
and  implies
implies 
-
 for all
for all  .
. -
 implies
implies  for all
for all  .
. - If
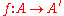 is an isomorphism and
is an isomorphism and  , then
, then  extends to an isomorphism
extends to an isomorphism  for some superset of
for some superset of  with
with 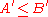 .
.
An embedding
 is strong if
is strong if 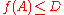 .
.We also want the pair (C,
 ) to satisfy the amalgamation property: if
) to satisfy the amalgamation property: if  then there is a
then there is a 
so that each
 embeds strongly into
embeds strongly into  with the same image for
with the same image for .
.For infinite
 , and
, and  , we say
, we say  iff
iff  for
for ,
,  . For any
. For any  , the
, theclosure of
 (in
(in  ),
), 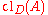 is the smallest superset of
is the smallest superset of 
satisfying
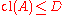 .
.Definition A countable structure
 is a (C,
is a (C,  )-generic if:
)-generic if:
- For
 ,
,  .
. - For
 , if
, if  then
then  there is a strong embedding of
there is a strong embedding of  into
into  over
over 
-
 has finite closures: for every
has finite closures: for every  ,
, 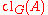 is finite.
is finite.
Theorem If (C,
 ) has the amalgamation property, then there is a unique (C,
) has the amalgamation property, then there is a unique (C,  )-generic.
)-generic.The existence proof proceeds in imitation of the existence proof for
Fraïssé limits. The uniqueness proof comes from an easy back and forth
argument.

