
Hooke's law
Overview
In mechanics
Mechanics
Mechanics is the branch of physics concerned with the behavior of physical bodies when subjected to forces or displacements, and the subsequent effects of the bodies on their environment....
, and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law is a useful approximation are known as linear-elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
or "Hookean" materials. Hooke's law in simple terms says that strain
Strain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
is directly proportional to stress.
Mathematically, Hooke's law states that
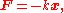
where
- x is the displacementDisplacement (vector)A displacement is the shortest distance from the initial to the final position of a point P. Thus, it is the length of an imaginary straight path, typically distinct from the path actually travelled by P...
of the spring's end from its equilibriumMechanical equilibriumA standard definition of static equilibrium is:This is a strict definition, and often the term "static equilibrium" is used in a more relaxed manner interchangeably with "mechanical equilibrium", as defined next....
position (a distance, in SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units: meters); - F is the restoring force exerted by the spring on that end (in SI units: N or kg·m/s2); and
- k is a constant called the rate or spring constant (in SI units: N/m or kg/s2).
When this holds, the behavior is said to be linear.

