In statistics

Statistics

Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....

, Hodges’ estimator (or Hodges–Le Cam estimator) is a famous counter example of an estimator

Estimator

In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....

 which is "superefficient", i.e. it attains smaller asymptotic variance than regular efficient estimators. The existence of such counterexample is the reason for the introduction of the notion of regular estimators.

Hodges’ estimator improves upon a regular estimator at a single point. In general, any superefficient estimator may surpass a regular estimator at most on a set of Lebesgue measure

Lebesgue measure

In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...

 zero.

Construction

Suppose $\backslash scriptstyle\backslash hat\backslash theta\_n$ is a "common" estimator for some parameter θ: it is consistent

Consistent estimator

In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...

, and converges to some asymptotic distribution

Asymptotic distribution

In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...

 L_θ (usually this is a normal distribution with mean zero and variance which may depend on θ) at the :

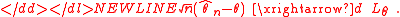
Then the Hodges’ estimator $\backslash scriptstyle\backslash hat\backslash theta^H\_n$ is defined as

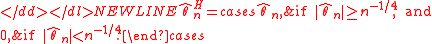
This estimator is equal to $\backslash scriptstyle\backslash hat\backslash theta\_n$ everywhere except on the small interval , where it is equal to zero. It is not difficult to see that this estimator is consistent

Consistent estimator

In statistics, a sequence of estimators for parameter θ0 is said to be consistent if this sequence converges in probability to θ0...

 for θ, and its asymptotic distribution

Asymptotic distribution

In mathematics and statistics, an asymptotic distribution is a hypothetical distribution that is in a sense the "limiting" distribution of a sequence of distributions...

 is

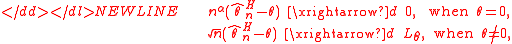
for any α ∈ R. Thus this estimator has the same asymptotic distribution as $\backslash scriptstyle\backslash hat\backslash theta\_n$ for all , whereas for the rate of convergence becomes arbitrarily fast. This estimator is superefficient, as it surpasses the asymptotic behavior of the efficient estimator $\backslash scriptstyle\backslash hat\backslash theta\_n$ at least at one point . In general, superefficiency may only be attained on a subset of measure zero of the parameter space Θ.

Example

Suppose x₁, …, x_n is an iid sample from normal distribution with unknown mean but known variance. Then the common estimator for the population mean θ is the arithmetic mean of all observations: $\backslash scriptstyle\backslash bar\{x\}$. The corresponding Hodges’ estimator will be $\backslash scriptstyle\backslash hat\backslash theta^H\_n\; \backslash ;=\backslash ;\; \backslash bar\{x\}\backslash cdot\backslash mathbf\{1\}\backslash \{|\backslash bar\; x|\backslash ,\backslash geq\backslash ,n^\{-1/4\}\backslash \}$, where 1{…} denotes the indicator function.

The mean square error (scaled by n) associated with the regular estimator x is constant and equal to 1 for all θ’s. At the same time the mean square error of the Hodges’ estimator $\backslash scriptstyle\backslash hat\backslash theta\_n^H$ behaves erratically in the vicinity of zero, and even becomes unbounded as . This demonstrates that the Hodges’ estimator is not regular, and its asymptotic properties are not adequately described by limits of the form (θ fixed).

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.