
Hilbert's theorem (differential geometry)
Encyclopedia
In differential geometry, Hilbert's theorem (1901) states that there exists no complete regular surface  of constant negative gaussian curvature
of constant negative gaussian curvature
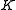 immersed in
immersed in  . This theorem answers the question for the negative case of which surfaces in
. This theorem answers the question for the negative case of which surfaces in 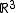 can be obtained by isometrically immersing complete manifolds with constant curvature
can be obtained by isometrically immersing complete manifolds with constant curvature
.
Hilbert's theorem was first treated by David Hilbert
in, "Über Flächen von konstanter Krümmung" (Trans. Amer. Math. Soc. 2 (1901), 87-99). A different proof was given shortly after by E. Holmgren, "Sur les surfaces à courbure constante negative," (1902).
s. The idea is to show the nonexistence of an isometric immersion
of a plane to the real space
to the real space  . This proof is basically the same as in Hilbert's paper, although based in the books of Do Carmo and Spivak
. This proof is basically the same as in Hilbert's paper, although based in the books of Do Carmo and Spivak
.
Observations: In order to have a more manageable treatment, but without loss of generality, the curvature
may be considered equal to minus one, . There is no loss of generality, since it is being dealt with constant curvatures, and similarities of
. There is no loss of generality, since it is being dealt with constant curvatures, and similarities of 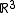 multiply
multiply 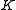 by a constant. The exponential map
by a constant. The exponential map
 is a local diffeomorphism
is a local diffeomorphism
, therefore, it induces an inner product in the tangent space
of at
at 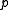 :
:  . Furthermore,
. Furthermore, 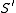 denotes the geometric surface
denotes the geometric surface  with this inner product. If
with this inner product. If  is an isometric immersion, the same holds for
is an isometric immersion, the same holds for .
.
The first lemma is independent from the other ones, and will be used at the end as the counter statement to reject the results from the other lemmas.
Lemma 1: The area of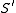 is infinite.
is infinite.
Proof's Sketch:
The idea of the proof is to create a global isometry between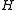 and
and  . Then, since
. Then, since  has an infinite area,
has an infinite area,  will have it too.
will have it too.
The fact that the hyperbolic plane
 has an infinite area comes by computing the surface integral
has an infinite area comes by computing the surface integral
with the corresponding coefficient
s of the First fundamental form
. To obtain these ones, the hyperbolic plane can be defined as the plane with the following inner product around a point with coordinates
with coordinates 

Since the hyperbolic plane is unbounded, the limits of the integral are infinite, and the area can be calculated through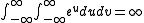
Next it is needed to create a map, which will show that the global information from the hyperbolic plane can be transfer to the surface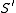 , i.e. a global isometry.
, i.e. a global isometry. 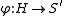 will be the map, whose domain is the hyperbolic plane and image the 2-dimensional manifold
will be the map, whose domain is the hyperbolic plane and image the 2-dimensional manifold  , which carries the inner product from the surface
, which carries the inner product from the surface 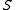 with negative curvature.
with negative curvature.  will be defined via the exponential map, its inverse, and a linear isometry between their tangent spaces,
will be defined via the exponential map, its inverse, and a linear isometry between their tangent spaces,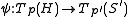 .
.
That is ,
,
where . That is to say, the starting point
. That is to say, the starting point 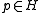 goes to the tangent plane from
goes to the tangent plane from  through the inverse of the exponential map. Then travels from one tangent plane to the other through the isometry
through the inverse of the exponential map. Then travels from one tangent plane to the other through the isometry 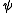 , and then down to the surface
, and then down to the surface 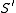 with another exponential map.
with another exponential map.
The following step involves the use of polar coordinates, and
and  , around
, around 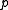 and
and  respectively. The requirement will be that the axis are mapped to each other, that is
respectively. The requirement will be that the axis are mapped to each other, that is  goes to
goes to  . Then
. Then  preserves the first fundamental form.
preserves the first fundamental form.
In a geodesic polar system, the Gaussian curvature
 can be expressed as
can be expressed as .
.
In addition K is constant and fulfills the following differential equation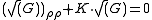
Since and
and  have the same constant Gaussian curvature, then they are locally isometric (Minding's Theorem). That means that
have the same constant Gaussian curvature, then they are locally isometric (Minding's Theorem). That means that  is a local isometry between
is a local isometry between 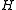 and
and 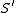 . Furthermore, from the Hadamard's theorem it follows that
. Furthermore, from the Hadamard's theorem it follows that  is also a covering map.
is also a covering map.
Since is simply connected,
is simply connected,  is a homeomorphism, and hence, a (global) isometry. Therefore,
is a homeomorphism, and hence, a (global) isometry. Therefore,  and
and 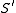 are globally isometric, and because
are globally isometric, and because 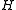 has an infinite area, then
has an infinite area, then  has an infinite area, as well.
has an infinite area, as well. 
Lemma 2: For each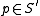 exists a parametrization
exists a parametrization 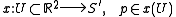 , such that the coordinate curves of
, such that the coordinate curves of  are asymptotic curves of
are asymptotic curves of  and form a Tchebyshef net.
and form a Tchebyshef net.
Lemma 3: Let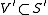 be a coordinate neighborhood of
be a coordinate neighborhood of  such that the coordinate curves are asymptotic curves in
such that the coordinate curves are asymptotic curves in 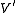 . Then the area A of any quadrilateral formed by the coordinate curves is smaller than
. Then the area A of any quadrilateral formed by the coordinate curves is smaller than  .
.
The next goal is to show that is a parametrization of
is a parametrization of  .
.
Lemma 4: For a fixed , the curve
, the curve 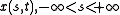 , is an asymptotic curve with
, is an asymptotic curve with  as arc length.
as arc length.
The following 2 lemmas together with lemma 8 will demonstrate the existence of a parametrization

Lemma 5: is a local diffeomorphism.
is a local diffeomorphism.
Lemma 6: is surjective.
is surjective.
Lemma 7: On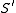 there are two differentiable linearly independent vector fields which are tangent to the asymptotic curve
there are two differentiable linearly independent vector fields which are tangent to the asymptotic curve
s of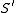 .
.
Lemma 8: is injective.
is injective.
Proof of Hilbert's Theorem:
First, it will be assumed that an isometric immersion from a complete surface with negative curvature exists:
exists: 
As stated in the observations, the tangent plane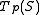 is endowed with the metric induced by the exponential map
is endowed with the metric induced by the exponential map  . Moreover,
. Moreover,  is an isometric immersion and Lemmas 5,6, and 8 show the existence of a parametrization
is an isometric immersion and Lemmas 5,6, and 8 show the existence of a parametrization  of the whole
of the whole 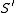 , such that the coordinate curves of
, such that the coordinate curves of  are the asymptotic curves of
are the asymptotic curves of 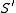 . This result was provided by Lemma 4. Therefore,
. This result was provided by Lemma 4. Therefore, 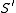 can be covered by a union of "coordinate" quadrilaterals
can be covered by a union of "coordinate" quadrilaterals 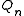 with
with  . By Lemma 3, the area of each quadrilateral is smaller than
. By Lemma 3, the area of each quadrilateral is smaller than  . On the other hand, by Lemma 1, the area of
. On the other hand, by Lemma 1, the area of  is infinite, therefore has no bounds. This is a contradiction and the proof is concluded.
is infinite, therefore has no bounds. This is a contradiction and the proof is concluded. 
 of constant negative gaussian curvature
of constant negative gaussian curvatureGaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
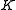 immersed in
immersed in  . This theorem answers the question for the negative case of which surfaces in
. This theorem answers the question for the negative case of which surfaces in 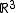 can be obtained by isometrically immersing complete manifolds with constant curvature
can be obtained by isometrically immersing complete manifolds with constant curvatureConstant curvature
In mathematics, constant curvature in differential geometry is a concept most commonly applied to surfaces. For those the scalar curvature is a single number determining the local geometry, and its constancy has the obvious meaning that it is the same at all points...
.
Hilbert's theorem was first treated by David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
in, "Über Flächen von konstanter Krümmung" (Trans. Amer. Math. Soc. 2 (1901), 87-99). A different proof was given shortly after by E. Holmgren, "Sur les surfaces à courbure constante negative," (1902).
Proof
The proof of Hilbert's theorem is elaborate and requires several lemmaLemma (mathematics)
In mathematics, a lemma is a proven proposition which is used as a stepping stone to a larger result rather than as a statement in-and-of itself...
s. The idea is to show the nonexistence of an isometric immersion

of a plane
 to the real space
to the real space  . This proof is basically the same as in Hilbert's paper, although based in the books of Do Carmo and Spivak
. This proof is basically the same as in Hilbert's paper, although based in the books of Do Carmo and SpivakMichael Spivak
Michael David Spivak is a mathematician specializing in differential geometry, an expositor of mathematics, and the founder of Publish-or-Perish Press. He is the author of the five-volume Comprehensive Introduction to Differential Geometry. He received a Ph.D...
.
Observations: In order to have a more manageable treatment, but without loss of generality, the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
may be considered equal to minus one,
 . There is no loss of generality, since it is being dealt with constant curvatures, and similarities of
. There is no loss of generality, since it is being dealt with constant curvatures, and similarities of 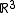 multiply
multiply 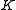 by a constant. The exponential map
by a constant. The exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
 is a local diffeomorphism
is a local diffeomorphismLocal diffeomorphism
In mathematics, more specifically differential topology, a local diffeomorphism is intuitively a function between smooth manifolds that preserves the local differentiable structure. The formal definition of a local diffeomorphism is given below....
, therefore, it induces an inner product in the tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
of
 at
at 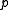 :
:  . Furthermore,
. Furthermore, 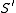 denotes the geometric surface
denotes the geometric surface  with this inner product. If
with this inner product. If  is an isometric immersion, the same holds for
is an isometric immersion, the same holds for .
.The first lemma is independent from the other ones, and will be used at the end as the counter statement to reject the results from the other lemmas.
Lemma 1: The area of
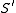 is infinite.
is infinite. Proof's Sketch:
The idea of the proof is to create a global isometry between
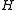 and
and  . Then, since
. Then, since  has an infinite area,
has an infinite area,  will have it too.
will have it too. The fact that the hyperbolic plane
Hyperbolic manifold
In mathematics, a hyperbolic n-manifold is a complete Riemannian n-manifold of constant sectional curvature -1.Every complete, connected, simply-connected manifold of constant negative curvature −1 is isometric to the real hyperbolic space Hn. As a result, the universal cover of any closed manifold...
 has an infinite area comes by computing the surface integral
has an infinite area comes by computing the surface integralSurface integral
In mathematics, a surface integral is a definite integral taken over a surface ; it can be thought of as the double integral analog of the line integral...
with the corresponding coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
s of the First fundamental form
First fundamental form
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
. To obtain these ones, the hyperbolic plane can be defined as the plane with the following inner product around a point
 with coordinates
with coordinates 

Since the hyperbolic plane is unbounded, the limits of the integral are infinite, and the area can be calculated through
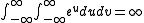
Next it is needed to create a map, which will show that the global information from the hyperbolic plane can be transfer to the surface
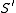 , i.e. a global isometry.
, i.e. a global isometry. 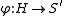 will be the map, whose domain is the hyperbolic plane and image the 2-dimensional manifold
will be the map, whose domain is the hyperbolic plane and image the 2-dimensional manifold  , which carries the inner product from the surface
, which carries the inner product from the surface 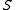 with negative curvature.
with negative curvature.  will be defined via the exponential map, its inverse, and a linear isometry between their tangent spaces,
will be defined via the exponential map, its inverse, and a linear isometry between their tangent spaces,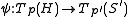 .
.That is
 ,
,where
 . That is to say, the starting point
. That is to say, the starting point 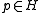 goes to the tangent plane from
goes to the tangent plane from  through the inverse of the exponential map. Then travels from one tangent plane to the other through the isometry
through the inverse of the exponential map. Then travels from one tangent plane to the other through the isometry 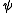 , and then down to the surface
, and then down to the surface 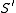 with another exponential map.
with another exponential map.The following step involves the use of polar coordinates,
 and
and  , around
, around 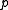 and
and  respectively. The requirement will be that the axis are mapped to each other, that is
respectively. The requirement will be that the axis are mapped to each other, that is  goes to
goes to  . Then
. Then  preserves the first fundamental form.
preserves the first fundamental form. In a geodesic polar system, the Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
 can be expressed as
can be expressed as .
.In addition K is constant and fulfills the following differential equation
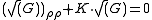
Since
 and
and  have the same constant Gaussian curvature, then they are locally isometric (Minding's Theorem). That means that
have the same constant Gaussian curvature, then they are locally isometric (Minding's Theorem). That means that  is a local isometry between
is a local isometry between 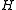 and
and 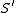 . Furthermore, from the Hadamard's theorem it follows that
. Furthermore, from the Hadamard's theorem it follows that  is also a covering map.
is also a covering map. Since
 is simply connected,
is simply connected,  is a homeomorphism, and hence, a (global) isometry. Therefore,
is a homeomorphism, and hence, a (global) isometry. Therefore,  and
and 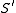 are globally isometric, and because
are globally isometric, and because 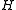 has an infinite area, then
has an infinite area, then  has an infinite area, as well.
has an infinite area, as well. 
Lemma 2: For each
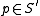 exists a parametrization
exists a parametrization 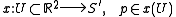 , such that the coordinate curves of
, such that the coordinate curves of  are asymptotic curves of
are asymptotic curves of  and form a Tchebyshef net.
and form a Tchebyshef net.Lemma 3: Let
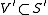 be a coordinate neighborhood of
be a coordinate neighborhood of  such that the coordinate curves are asymptotic curves in
such that the coordinate curves are asymptotic curves in 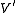 . Then the area A of any quadrilateral formed by the coordinate curves is smaller than
. Then the area A of any quadrilateral formed by the coordinate curves is smaller than  .
.The next goal is to show that
 is a parametrization of
is a parametrization of  .
.Lemma 4: For a fixed
 , the curve
, the curve 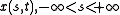 , is an asymptotic curve with
, is an asymptotic curve with  as arc length.
as arc length.The following 2 lemmas together with lemma 8 will demonstrate the existence of a parametrization
Parametrization
Parametrization is the process of deciding and defining the parameters necessary for a complete or relevant specification of a model or geometric object....

Lemma 5:
 is a local diffeomorphism.
is a local diffeomorphism.Lemma 6:
 is surjective.
is surjective.Lemma 7: On
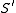 there are two differentiable linearly independent vector fields which are tangent to the asymptotic curve
there are two differentiable linearly independent vector fields which are tangent to the asymptotic curveAsymptotic curve
In the differential geometry of surfaces, an asymptotic curve is a curve always tangent to an asymptotic direction of the surface . It is sometimes called an asymptotic line, although it need not be a line....
s of
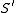 .
.Lemma 8:
 is injective.
is injective. Proof of Hilbert's Theorem:
First, it will be assumed that an isometric immersion from a complete surface with negative curvature
 exists:
exists: 
As stated in the observations, the tangent plane
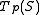 is endowed with the metric induced by the exponential map
is endowed with the metric induced by the exponential map  . Moreover,
. Moreover,  is an isometric immersion and Lemmas 5,6, and 8 show the existence of a parametrization
is an isometric immersion and Lemmas 5,6, and 8 show the existence of a parametrization  of the whole
of the whole 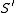 , such that the coordinate curves of
, such that the coordinate curves of  are the asymptotic curves of
are the asymptotic curves of 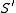 . This result was provided by Lemma 4. Therefore,
. This result was provided by Lemma 4. Therefore, 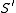 can be covered by a union of "coordinate" quadrilaterals
can be covered by a union of "coordinate" quadrilaterals 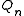 with
with  . By Lemma 3, the area of each quadrilateral is smaller than
. By Lemma 3, the area of each quadrilateral is smaller than  . On the other hand, by Lemma 1, the area of
. On the other hand, by Lemma 1, the area of  is infinite, therefore has no bounds. This is a contradiction and the proof is concluded.
is infinite, therefore has no bounds. This is a contradiction and the proof is concluded. 

