
Hilbert's nineteenth problem
Encyclopedia
Hilbert's nineteenth problem is one of the 23 Hilbert problems set out in a celebrated list compiled in 1900 by David Hilbert
. It asks whether the solutions of regular problems in the calculus of variations are always analytic
.
gave a counterexample showing that in the case when the solution is vector-valued rather than scalar-valued, the solution need not be analytic.
stating that if u is a solution of a suitable linear second order strictly elliptic PDE of the form
and u has square integrable first derivatives, then u is Hölder continuous.
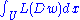
are analytic. Here w is a function on some compact set U of Rn, Dw is the vector of its first derivatives, and L is the Lagrangian, a function of the derivatives of w that satisfies certain growth, smoothness, and convexity conditions. The smoothness of w can be shown using De Giorgi's theorem
as follows. The Euler-Lagrange equation for this variational problem is the non-linear equation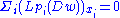
and differentiating this with respect to xk gives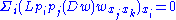
This means that u=wxk satisfies the linear equation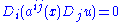
with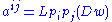
so by De Giorgi's result the solution w has Hölder continuous first derivatives.
Once w is known to have Hölder continuous (n+1)st derivatives for some n ≥ 0, then the coefficients aij have Hölder continuous nth derivatives, so a theorem of Schauder implies that the (n+2)nd derivatives are also Hölder continuous, so repeating this infinitely often shows that the solution w is smooth.
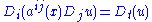
where u is a bounded function of x1,...,xn, t defined for t ≥ 0. From his estimate Nash was able to deduce a continuity estimate for solutions of the elliptic equation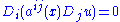 by considering the special case when u does not depend on t.
by considering the special case when u does not depend on t.
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
. It asks whether the solutions of regular problems in the calculus of variations are always analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
.
History
For C3 solutions Hilbert's problem was answered positively by in his thesis, who showed that C3 solutions of nonlinear elliptic analytic equations in 2 variables are analytic. Bernstein's result was improved over the years by several authors, such as , who reduced the differentiability requirements on the solution needed to prove that it is analytic. On the other hand direct methods in the calculus of variations showed the existence of solutions with very weak differentiability properties. For many years there was a gap between these results: the solutions that could be constructed were known to have square integrable second derivatives, which was not quite strong enough to feed into the machinery that could prove they were analytic, which needed continuity of first derivatives. This gap was filled independently by , and . They were able to show the solutions had first derivatives that were Hölder continuous, which by previous results implied that the solutions are analytic whenever the differential equation has analytic coefficients, thus completing the solution of Hilbert's nineteenth problem.gave a counterexample showing that in the case when the solution is vector-valued rather than scalar-valued, the solution need not be analytic.
De Giorgi's theorem
The key theorem proved by De Giorgi is an a priori estimateA priori estimate
In the theory of partial differential equations, an a priori estimate is an estimate for the size of a solution or its derivatives of a partial differential equation. A priori is Latin for "from before" and refers to the fact that the estimate for the solution is derived before the solution is...
stating that if u is a solution of a suitable linear second order strictly elliptic PDE of the form

and u has square integrable first derivatives, then u is Hölder continuous.
Application of De Giorgi's theorem to Hilbert's problem
Hilbert's problem asks whether the minimizers w of an energy functional such as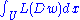
are analytic. Here w is a function on some compact set U of Rn, Dw is the vector of its first derivatives, and L is the Lagrangian, a function of the derivatives of w that satisfies certain growth, smoothness, and convexity conditions. The smoothness of w can be shown using De Giorgi's theorem
as follows. The Euler-Lagrange equation for this variational problem is the non-linear equation
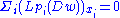
and differentiating this with respect to xk gives
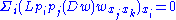
This means that u=wxk satisfies the linear equation
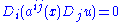
with
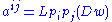
so by De Giorgi's result the solution w has Hölder continuous first derivatives.
Once w is known to have Hölder continuous (n+1)st derivatives for some n ≥ 0, then the coefficients aij have Hölder continuous nth derivatives, so a theorem of Schauder implies that the (n+2)nd derivatives are also Hölder continuous, so repeating this infinitely often shows that the solution w is smooth.
Nash's theorem
Nash gave a continuity estimate for solutions of the parabolic equation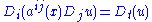
where u is a bounded function of x1,...,xn, t defined for t ≥ 0. From his estimate Nash was able to deduce a continuity estimate for solutions of the elliptic equation
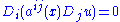 by considering the special case when u does not depend on t.
by considering the special case when u does not depend on t.

