Heun's method
Encyclopedia
In mathematics
and computational science
, Heun's method may refer to the improved or modified Euler's method (that is, the explicit trapezoidal rule), or a similar two-stage Runge–Kutta method. It is named after Karl L. W. M. Heun and is a numerical
procedure for solving ordinary differential equations
(ODEs) with a given initial value
. Both variants can be seen as extensions of the Euler method into two-stage second-order Runge–Kutta methods.
The procedure for calculating the numerical solution to the initial value problem via the improved Euler's method is:
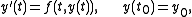
by way of Heun's method, is to first calculate the intermediate value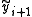
and then the final approximation 
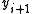at the next integration point.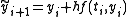
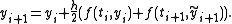
trapezoidal method, but with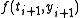
replaced by 
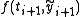in order to make it explicit. 
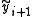is the result of one step of Euler's method on the same initial value problem.
So, Heun's method is a predictor-corrector method
with forward Euler's method as predictor and trapezoidal method as corrector.
):
The other method referred to as Heun's method has the Butcher table:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and computational science
Computational science
Computational science is the field of study concerned with constructing mathematical models and quantitative analysis techniques and using computers to analyze and solve scientific problems...
, Heun's method may refer to the improved or modified Euler's method (that is, the explicit trapezoidal rule), or a similar two-stage Runge–Kutta method. It is named after Karl L. W. M. Heun and is a numerical
Numerical analysis
Numerical analysis is the study of algorithms that use numerical approximation for the problems of mathematical analysis ....
procedure for solving ordinary differential equations
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
(ODEs) with a given initial value
Initial value problem
In mathematics, in the field of differential equations, an initial value problem is an ordinary differential equation together with a specified value, called the initial condition, of the unknown function at a given point in the domain of the solution...
. Both variants can be seen as extensions of the Euler method into two-stage second-order Runge–Kutta methods.
The procedure for calculating the numerical solution to the initial value problem via the improved Euler's method is:
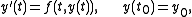
by way of Heun's method, is to first calculate the intermediate value
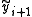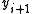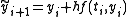
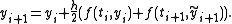
and then the final approximation at the next integration point.Derivation
The scheme can be compared with the implicitExplicit and implicit methods
Explicit and implicit methods are approaches used in numerical analysis for obtaining numerical solutions of time-dependent ordinary and partial differential equations, as is required in computer simulations of physical processes....
trapezoidal method, but with
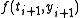replaced by 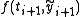in order to make it explicit. 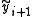is the result of one step of Euler's method on the same initial value problem.So, Heun's method is a predictor-corrector method
Predictor-corrector method
In mathematics, particularly numerical analysis, a predictor–corrector method is an algorithm that proceeds in two steps. First, the prediction step calculates a rough approximation of the desired quantity...
with forward Euler's method as predictor and trapezoidal method as corrector.
Runge–Kutta method
The improved Euler's method is a two-stage Runge–Kutta method, and can be written using the Butcher tableau (after John C. ButcherJohn C. Butcher
John Charles Butcher is a mathematician who specialises in numerical methods for the solution of ordinary differential equations. Butcher works on multistage methods for initial value problems, such as Runge-Kutta and general linear methods...
):
| 0 | ||
| | 1 | 1 | |
| | | 1/2 | 1/2 |
The other method referred to as Heun's method has the Butcher table:
| 0 | ||
| | 2/3 | 1 | |
| | | 1/4 | 3/4 |