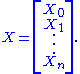Hermitian variety
Encyclopedia
Hermitian varieties are in a sense a generalisation of quadric
s, and occur naturally in the theory of polarities.
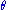 . Let n be an integer
. Let n be an integer 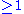 and V be an (n+1)-dimensional vectorspace over K.
and V be an (n+1)-dimensional vectorspace over K.
A Hermitian variety H in PG(V) is a set of points of which the representing vector lines consisting of isotropic points of a non-trivial Hermitian sesquilinear form on V.
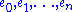 be a basis of V. If a point p in the projective space
be a basis of V. If a point p in the projective space
has homogenous coordinates with respect to this basis, it is on the Hermitian variety if and only if :
with respect to this basis, it is on the Hermitian variety if and only if :
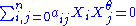
where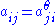 and not all
and not all 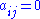
If one construct the Hermitian matrix A with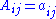 , the equation can be written in a compact way :
, the equation can be written in a compact way :
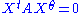
where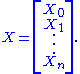
Quadric
In mathematics, a quadric, or quadric surface, is any D-dimensional hypersurface in -dimensional space defined as the locus of zeros of a quadratic polynomial...
s, and occur naturally in the theory of polarities.
Definition
Let K be a field with an involutive automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
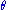 . Let n be an integer
. Let n be an integer 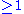 and V be an (n+1)-dimensional vectorspace over K.
and V be an (n+1)-dimensional vectorspace over K.A Hermitian variety H in PG(V) is a set of points of which the representing vector lines consisting of isotropic points of a non-trivial Hermitian sesquilinear form on V.
Representation
Let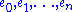 be a basis of V. If a point p in the projective space
be a basis of V. If a point p in the projective spaceProjective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
has homogenous coordinates
 with respect to this basis, it is on the Hermitian variety if and only if :
with respect to this basis, it is on the Hermitian variety if and only if :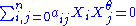
where
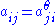 and not all
and not all 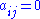
If one construct the Hermitian matrix A with
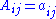 , the equation can be written in a compact way :
, the equation can be written in a compact way :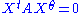
where