
Hermitian hat wavelet
Encyclopedia
The Hermitian hat wavelet is a low-oscillation
, complex-valued wavelet
.
The real and imaginary parts of this wavelet are defined to be the
second and first derivative
s of a Gauss
ian respectively:
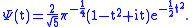
The Fourier transform
of this wavelet is:
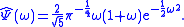
The Hermitian hat wavelet satisfies the admissibility criterion. The prefactor in the resolution of the identity of the continuous wavelet transform is:
in the resolution of the identity of the continuous wavelet transform is:
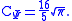
This wavelet was formulated by Szu in 1997 for the numerical estimation of
function derivatives in the presence of noise. The
technique used to extract these derivative values exploits only the
argument (phase) of the wavelet and, consequently, the relative weights
of the real and imaginary parts are unimportant.
Oscillation
Oscillation is the repetitive variation, typically in time, of some measure about a central value or between two or more different states. Familiar examples include a swinging pendulum and AC power. The term vibration is sometimes used more narrowly to mean a mechanical oscillation but sometimes...
, complex-valued wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
.
The real and imaginary parts of this wavelet are defined to be the
second and first derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
s of a Gauss
Gauss
Gauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
ian respectively:
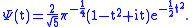
The Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of this wavelet is:
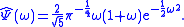
The Hermitian hat wavelet satisfies the admissibility criterion. The prefactor
 in the resolution of the identity of the continuous wavelet transform is:
in the resolution of the identity of the continuous wavelet transform is: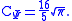
This wavelet was formulated by Szu in 1997 for the numerical estimation of
function derivatives in the presence of noise. The
technique used to extract these derivative values exploits only the
argument (phase) of the wavelet and, consequently, the relative weights
of the real and imaginary parts are unimportant.

