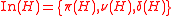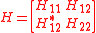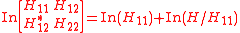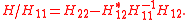Haynsworth inertia additivity formula
Encyclopedia
In mathematics, the Haynsworth inertia additivity formula, discovered by Emilie Virginia Haynsworth (1916–1985), concerns the number of positive, negative, and zero eigenvalues of a Hermitian matrix and of block matrices into which it is partitioned
.
The inertia of a Hermitian matrix H is defined as the ordered triple
whose components are respectively the numbers of positive, negative, and zero eigenvalues of H. Haynsworth considered a partitioned Hermitian matrix
where H11 is nonsingular and H12* is the conjugate transpose
of H12. The formula states:http://books.google.com/books?id=Wjd8_AwjiIIC&pg=PA15&lpg=PA15&dq=haynsworth+inertia&source=bl&ots=jpVOPR63Ps&sig=C7H_0a44_aC2RKpKuM91zHdKEaI&hl=en&ei=4SazTa6lCemW0QGg6_WzCQ&sa=X&oi=book_result&ct=result&resnum=3&sqi=2&ved=0CCQQ6AEwAg#v=onepage&q=haynsworth%20inertia&f=false
where H/H11 is the Schur complement
of H11 in H:
The formula does not hold if H11 is singular. However, a generalization has been proven in 1974 by Carlson, Haynsworth and Markham , to the effect that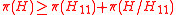 and
and 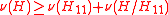 .
.
Carlson, Haynsworth and Markham also gave sufficient and necessary conditions for equality to hold.
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
.
The inertia of a Hermitian matrix H is defined as the ordered triple
whose components are respectively the numbers of positive, negative, and zero eigenvalues of H. Haynsworth considered a partitioned Hermitian matrix
where H11 is nonsingular and H12* is the conjugate transpose
Conjugate transpose
In mathematics, the conjugate transpose, Hermitian transpose, Hermitian conjugate, or adjoint matrix of an m-by-n matrix A with complex entries is the n-by-m matrix A* obtained from A by taking the transpose and then taking the complex conjugate of each entry...
of H12. The formula states:http://books.google.com/books?id=Wjd8_AwjiIIC&pg=PA15&lpg=PA15&dq=haynsworth+inertia&source=bl&ots=jpVOPR63Ps&sig=C7H_0a44_aC2RKpKuM91zHdKEaI&hl=en&ei=4SazTa6lCemW0QGg6_WzCQ&sa=X&oi=book_result&ct=result&resnum=3&sqi=2&ved=0CCQQ6AEwAg#v=onepage&q=haynsworth%20inertia&f=false
where H/H11 is the Schur complement
Schur complement
In linear algebra and the theory of matrices,the Schur complement of a matrix block is defined as follows.Suppose A, B, C, D are respectivelyp×p, p×q, q×p...
of H11 in H:
Generalization
If H11 is singular, we can still define the generalized Schur complement, using the Moore–Penrose inverse instead of .The formula does not hold if H11 is singular. However, a generalization has been proven in 1974 by Carlson, Haynsworth and Markham , to the effect that
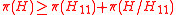 and
and 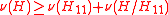 .
.Carlson, Haynsworth and Markham also gave sufficient and necessary conditions for equality to hold.