Hasse–Arf theorem
Encyclopedia
In mathematics
, specifically in local class field theory, the Hasse–Arf theorem is a result concerning jumps of a filtration of the Galois group
of a finite Galois extension
. A special case of it was originally proved by Helmut Hasse
, and the general result was proved by Cahit Arf
.
L/K. So assume L/K is a finite Galois extension, and that vK is a discrete normalised valuation of K, whose residue field has characteristic p > 0, and which admits a unique extension to L, say w. Denote by vL the associated normalised valuation ew of L and let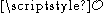 be the valuation ring
be the valuation ring
of L under vL. Let L/K have Galois group
G and define the s-th ramification group of L/K for any real s ≥ −1 by
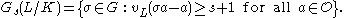
So, for example, G−1 is the Galois group G. To pass to the upper numbering one has to define the function ψL/K which in turn is the inverse of the function ηL/K defined by
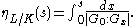
The upper numbering of the ramification group
s is then defined by Gt(L/K) = Gs(L/K) where s = ψL/K(t).
These higher ramification groups Gt(L/K) are defined for any real t ≥ −1, but since vL is a discrete valuation, the groups will change in discrete jumps and not continuously. Thus we say that t is a jump of the filtration {Gt(L/K) : t ≥ −1} if Gt(L/K) ≠ Gu(L/K) for any u > t. The Hasse–Arf theorem tells us the arithmetic nature of these jumps
.
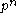 ,
, 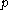 residue characteristic and
residue characteristic and 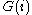 be the subgroup of
be the subgroup of 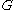 of order
of order  . The the theorem says that there exist positive integers
. The the theorem says that there exist positive integers  such that
such that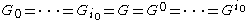

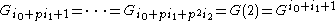
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in local class field theory, the Hasse–Arf theorem is a result concerning jumps of a filtration of the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of a finite Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
. A special case of it was originally proved by Helmut Hasse
Helmut Hasse
Helmut Hasse was a German mathematician working in algebraic number theory, known for fundamental contributions to class field theory, the application of p-adic numbers to local classfield theory and diophantine geometry , and to local zeta functions.-Life:He was born in Kassel, and died in...
, and the general result was proved by Cahit Arf
Cahit Arf
Cahit Arf was a Turkish mathematician. He is known for the Arf invariant of a quadratic form in characteristic 2 in topology, the Hasse–Arf theorem in ramification theory, Arf semigroups, and Arf rings.-Biography:Cahit Arf was born on 11 October 1910 in Selanik , which was then...
.
Higher ramification groups
The theorem deals with the upper numbered higher ramification groups of a finite abelian extensionAbelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
L/K. So assume L/K is a finite Galois extension, and that vK is a discrete normalised valuation of K, whose residue field has characteristic p > 0, and which admits a unique extension to L, say w. Denote by vL the associated normalised valuation ew of L and let
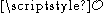 be the valuation ring
be the valuation ringValuation ring
In abstract algebra, a valuation ring is an integral domain D such that for every element x of its field of fractions F, at least one of x or x −1 belongs to D....
of L under vL. Let L/K have Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
G and define the s-th ramification group of L/K for any real s ≥ −1 by
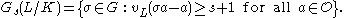
So, for example, G−1 is the Galois group G. To pass to the upper numbering one has to define the function ψL/K which in turn is the inverse of the function ηL/K defined by
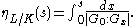
The upper numbering of the ramification group
Ramification group
In number theory, more specifically in local class field theory, the ramification groups are a filtration of the Galois group of a local field extension, which gives a precisely information on the ramification phenomenon of the extension....
s is then defined by Gt(L/K) = Gs(L/K) where s = ψL/K(t).
These higher ramification groups Gt(L/K) are defined for any real t ≥ −1, but since vL is a discrete valuation, the groups will change in discrete jumps and not continuously. Thus we say that t is a jump of the filtration {Gt(L/K) : t ≥ −1} if Gt(L/K) ≠ Gu(L/K) for any u > t. The Hasse–Arf theorem tells us the arithmetic nature of these jumps
Statement of the theorem
With the above set up, the theorem states that the jumps of the filtration {Gt(L/K) : t ≥ −1} are all rational integersInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
.
Example
Suppose G is cyclic of order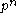 ,
, 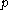 residue characteristic and
residue characteristic and 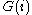 be the subgroup of
be the subgroup of 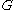 of order
of order  . The the theorem says that there exist positive integers
. The the theorem says that there exist positive integers  such that
such that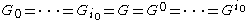

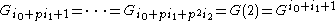
- ...