
Hartley function
Encyclopedia
The Hartley function is a measure of uncertainty, introduced by Ralph Hartley
in 1928. If we pick a sample from a finite set A uniformly at random, the information revealed after we know the outcome is given by the Hartley function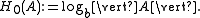
If the base of the logarithm
is 2, then the uncertainty is measured in bits. If it is the natural logarithm
, then the unit is nats
. (Hartley himself used a base-ten logarithm, and this unit of information is sometimes called the hartley
in his honor.) It is also known as the Hartley entropy.
since: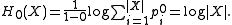
But it can also be viewed as a primitive construction, since, as emphasized by Kolmogorov and Rényi (see George, J. Klirr's "Uncertainty and information", p.423), the Hartley function can be defined without introducing any notions of probability.
Condition 1 says that the uncertainty of the Cartesian product of two finite sets A and B is the sum of uncertainties of A and B. Condition 2 says that larger set has larger uncertainty.
Let ƒ be a function on positive integers that satisfies the above three properties. From the additive property, we can show that for any integer n and k,
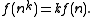
Let a, b, and t be any positive integers. There is a unique integer s determined by
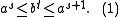
Therefore,

and

On the other hand, by monotonicity,
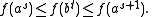
Using Equation (1), we get
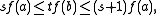
and

Hence,

Since t can be arbitrarily large, the difference on the left hand side of the above inequality must be zero,
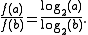
So,
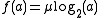
for some constant μ, which must be equal to 1 by the normalization property.
Ralph Hartley
Ralph Vinton Lyon Hartley was an electronics researcher. He invented the Hartley oscillator and the Hartley transform, and contributed to the foundations of information theory.-Biography:...
in 1928. If we pick a sample from a finite set A uniformly at random, the information revealed after we know the outcome is given by the Hartley function
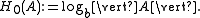
If the base of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
is 2, then the uncertainty is measured in bits. If it is the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
, then the unit is nats
Nat (information)
A nat is a logarithmic unit of information or entropy, based on natural logarithms and powers of e, rather than the powers of 2 and base 2 logarithms which define the bit. The nat is the natural unit for information entropy...
. (Hartley himself used a base-ten logarithm, and this unit of information is sometimes called the hartley
Ban (information)
A ban, sometimes called a hartley or a dit , is a logarithmic unit which measures information or entropy, based on base 10 logarithms and powers of 10, rather than the powers of 2 and base 2 logarithms which define the bit. As a bit corresponds to a binary digit, so a ban is a decimal digit...
in his honor.) It is also known as the Hartley entropy.
Hartley function, Shannon's entropy, and Rényi entropy
The Hartley function coincides with the Shannon entropy (as well as with the Rényi entropies of all orders) in the case of a uniform probability distribution. It is actually a special case of the Rényi entropyRényi entropy
In information theory, the Rényi entropy, a generalisation of Shannon entropy, is one of a family of functionals for quantifying the diversity, uncertainty or randomness of a system...
since:
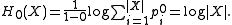
But it can also be viewed as a primitive construction, since, as emphasized by Kolmogorov and Rényi (see George, J. Klirr's "Uncertainty and information", p.423), the Hartley function can be defined without introducing any notions of probability.
Characterization of the Hartley function
The Hartley function only depends on the number of elements in a set, and hence can be viewed as a function on natural numbers. Rényi showed that the Hartley function in base 2 is the only function mapping natural numbers to real numbers that satisfies-
 (additivity)
(additivity) -
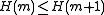 (monotonicity)
(monotonicity) -
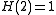 (normalization)
(normalization)
Condition 1 says that the uncertainty of the Cartesian product of two finite sets A and B is the sum of uncertainties of A and B. Condition 2 says that larger set has larger uncertainty.
Derivation of the Hartley function
We want to show that the Hartley function, log2(n), is the only function mapping natural numbers to real numbers that satisfies-
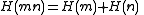 (additivity)
(additivity) -
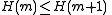 (monotonicity)
(monotonicity) -
 (normalization)
(normalization)
Let ƒ be a function on positive integers that satisfies the above three properties. From the additive property, we can show that for any integer n and k,
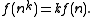
Let a, b, and t be any positive integers. There is a unique integer s determined by
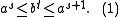
Therefore,

and

On the other hand, by monotonicity,
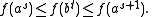
Using Equation (1), we get
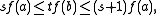
and

Hence,

Since t can be arbitrarily large, the difference on the left hand side of the above inequality must be zero,
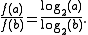
So,
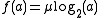
for some constant μ, which must be equal to 1 by the normalization property.

