Hardy's theorem
Encyclopedia
In mathematics
, Hardy's theorem is a result in complex analysis
describing the behavior of holomorphic function
s.
Let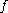
be a holomorphic function on the open ball centered at zero and radius 
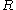in the complex plane
, and assume that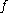
is not a constant function
. If one defines
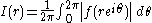
for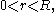
then this function is strictly increasing
and logarithmically convex
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Hardy's theorem is a result in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
describing the behavior of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s.
Let
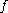be a holomorphic function on the open ball centered at zero and radius 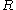in the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, and assume that
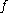is not a constant functionConstant function
In mathematics, a constant function is a function whose values do not vary and thus are constant. For example the function f = 4 is constant since f maps any value to 4...
. If one defines
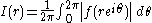
for
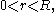then this function is strictly increasingMonotonic function
In mathematics, a monotonic function is a function that preserves the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order theory....
and logarithmically convex
Logarithmically convex function
In mathematics, a function f defined on a convex subset of a real vector space and taking positive values is said to be logarithmically convex if \log f is a convex function of x....
.