
Hagedorn temperature
Encyclopedia
The Hagedorn temperature in theoretical physics
is the temperature above which the partition sum diverges in a system with exponential growth in the density of states. It is named after German physicist Rolf Hagedorn
.
Phase transitions (e.g. from a solid state of matter to that of a liquid one) are in general possible only when the system has a higher number of particles than is thought possible. Such behavior surprised many in the world of elementary particle systems. However, as signaled by abundant particle production present in strong interactions, the quark structure of strongly interacting particles allows an infinite number of "degrees of freedom" to be present in finite volume. In other words, a highly relativistic system can produce pairs
and thus effectively be of infinite size.
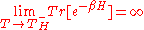
Because of the divergence, it seemed at first impossible to have temperatures above the Hagedorn temperature, which would make it the absolute hot
temperature, because it would require an infinite amount of energy
. In equations:
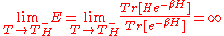
This line of reasoning has been improved in work of Hagedorn and Johann Rafelski
, where it was shown that instead a phase transition to quark matter occurs.
interactions. The idea of applying the wide body of knowledge of statistical thermodynamics to such multi-particle production processes naturally comes to mind and prominent physicists like Enrico Fermi
and Lev Landau
made pioneering contributions. However, difficulties quickly speak for themselves, and this approach did not become the main stream of the study of particle production at first. The question was, what might actually be "thermalized" in a high energy particle collision? Applying straightforward statistical mechanics gave too small a yield of pions. But, even if there was a thermalized system in the first place, why was the apparent temperature constant, shouldn't one expect it to rise with incident beam energy? It is Hagedorn's great credit that he proposed the right model and stayed with his thermal interpretation, solving the mysteries one after the other. His particle production models turned out to be remarkably accurate at predicting yields for the many different types of secondaries which originate from high energy collisions. He understood that the temperature governing particle spectra does not increase, since as more and more energy is poured into the system, new particles are produced. It is the entropy
which increases with the collision energy. If the number of particles of given mass (mass spectrum) increases exponentially, the temperature gets stuck to a limiting value. This is the Hagedorn temperature. It is in particle units nearly kT=160 MeV, about 15% above the energy mass of the lightest hadron, the pion. Moreover, since more massive particles fragment into less massive ones, and eventually give the observed secondary particles as the bottom line, this solved the pion yield problem.
assures that all constituents are relatively weakly interacting. There seemed to be nothing that would stop a dense assembly of hadrons from dissolving into a plasma of quarks and gluons. This new state of matter could be heated to a very high temperature and no limit was in sight. What is the meaning of Hagedorn temperature in this enlarged context?
In the SBM as conceived before quarks, hadrons were point particles. Now a subtle modification is required when considering quarks as building blocks. Hadrons made of quarks need a finite proper volume growing with hadron mass. Hagedorn and Rafelski discovered that at the Hagedorn temperature finite size hadrons dissolve into a quark-gluon liquid. Both a phase transition and a smoother transformation is possible, depending on the precise nature of the mass spectrum. The most physically attractive alternative was a first order phase transition. In this case the latent heat is delivered to the hadron phase at a constant Hagedorn temperature. One then reaches a new phase wherein the hadron constituents, the quarks and the gluons, are no longer confined. The system temperature can now rise again.
(QGP).
. It was incorporated into high-energy physics in mid 1960. In hadronic physics, the Hagedorn temperature is today understood to be the deconfinement temperature of quarks, while in string theory, it indicates another phase transition: the transition at which very long strings are copiously produced. It is controlled by the size of the string tension which is smaller than the Planck scale by the some power of the coupling constant. By adjusting the tension to be small compared to the Planck scale, the Hagedorn transition can be much less than the Planck temperature
. Traditional grand-unified string models place this in the magnitude of 1030 kelvin
, two orders of magnitude smaller than the Planck temperature.
Theoretical physics
Theoretical physics is a branch of physics which employs mathematical models and abstractions of physics to rationalize, explain and predict natural phenomena...
is the temperature above which the partition sum diverges in a system with exponential growth in the density of states. It is named after German physicist Rolf Hagedorn
Rolf Hagedorn
Rolf Hagedorn was a German theoretical physicists working at CERN. He is known for the idea that hadronic matter has a "melting point". The Hagedorn temperature is named in his honor.-Early life:...
.
Phase transitions (e.g. from a solid state of matter to that of a liquid one) are in general possible only when the system has a higher number of particles than is thought possible. Such behavior surprised many in the world of elementary particle systems. However, as signaled by abundant particle production present in strong interactions, the quark structure of strongly interacting particles allows an infinite number of "degrees of freedom" to be present in finite volume. In other words, a highly relativistic system can produce pairs
Pair production
Pair production refers to the creation of an elementary particle and its antiparticle, usually from a photon . For example an electron and its antiparticle, the positron, may be created...
and thus effectively be of infinite size.
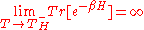
Because of the divergence, it seemed at first impossible to have temperatures above the Hagedorn temperature, which would make it the absolute hot
Absolute hot
Absolute hot is a concept of temperature that postulates the existence of a highest attainable temperature of matter. The idea has been popularized by the television series Nova...
temperature, because it would require an infinite amount of energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
. In equations:
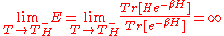
This line of reasoning has been improved in work of Hagedorn and Johann Rafelski
Johann Rafelski
Johann Rafelski is a German-American theoretical physicist and author. He is Professor of Physics at The University of Arizona in Tucson, guest scientist at CERN , and has been LMU-Excellent Guest Professor at the Ludwig Maximilian University of Munich in Munich, Germany.Rafelski’s current...
, where it was shown that instead a phase transition to quark matter occurs.
The Boiling hadron Matter
Very high energy collisions generally result in the production of many secondary particles. This was an unexpected feature when it was first observed in cosmic rayCosmic ray
Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...
interactions. The idea of applying the wide body of knowledge of statistical thermodynamics to such multi-particle production processes naturally comes to mind and prominent physicists like Enrico Fermi
Enrico Fermi
Enrico Fermi was an Italian-born, naturalized American physicist particularly known for his work on the development of the first nuclear reactor, Chicago Pile-1, and for his contributions to the development of quantum theory, nuclear and particle physics, and statistical mechanics...
and Lev Landau
Lev Landau
Lev Davidovich Landau was a prominent Soviet physicist who made fundamental contributions to many areas of theoretical physics...
made pioneering contributions. However, difficulties quickly speak for themselves, and this approach did not become the main stream of the study of particle production at first. The question was, what might actually be "thermalized" in a high energy particle collision? Applying straightforward statistical mechanics gave too small a yield of pions. But, even if there was a thermalized system in the first place, why was the apparent temperature constant, shouldn't one expect it to rise with incident beam energy? It is Hagedorn's great credit that he proposed the right model and stayed with his thermal interpretation, solving the mysteries one after the other. His particle production models turned out to be remarkably accurate at predicting yields for the many different types of secondaries which originate from high energy collisions. He understood that the temperature governing particle spectra does not increase, since as more and more energy is poured into the system, new particles are produced. It is the entropy
Entropy
Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
which increases with the collision energy. If the number of particles of given mass (mass spectrum) increases exponentially, the temperature gets stuck to a limiting value. This is the Hagedorn temperature. It is in particle units nearly kT=160 MeV, about 15% above the energy mass of the lightest hadron, the pion. Moreover, since more massive particles fragment into less massive ones, and eventually give the observed secondary particles as the bottom line, this solved the pion yield problem.
The Statistical Bootstrap Model (SBM)
Hagedorn next addressed the experimental fact that resonance formation dominates the scattering cross section and proposed the Statistical Bootstrap Model (SBM). To put SBM in a nutshell one may say that each of the many resonant state into which hadrons can be excited through a collision is itself a constituent of a still heavier resonance, while being also composed of lighter ones. In this way, a matter cluster consisting of hadron resonances becomes a constituent cluster when compressed to its natural volume: fireballs going into fireballs living on fireballs forever and all in a logically very consistent way. Hagedorn obtained within the SBM approach to a strongly interacting system an exponential rising mass spectrum of resonant states. Experimental results for hadronic level counting can now be followed up to nearly 5000 cataloged resonances. They agree beautifully with theoretical SBM expectations. As our knowledge has increased, the observed mass spectrum has become a better exponential. As time has gone by, the understanding of particle production process brought about by Hagedorn has grown in significance. Hagedorn's article which introduces the statistical bootstrap model of particle production, and places the maximum temperature in the particle physics vocabulary has found a place among the most cited physics papers.Transition to Quark-Gluon Plasma
In parallel to the SBM development the newly discovered quarks became progressively more trusted building blocks of hadrons. Hagedorn saw a compressed gas of hadrons as another hadron. In the quark picture this is, however, a drop of quark matter. In quark matter at high temperature gluons would also be present and as temperature is increased, asymptotic freedomAsymptotic freedom
In physics, asymptotic freedom is a property of some gauge theories that causes interactions between particles to become arbitrarily weak at energy scales that become arbitrarily large, or, equivalently, at length scales that become arbitrarily small .Asymptotic freedom is a feature of quantum...
assures that all constituents are relatively weakly interacting. There seemed to be nothing that would stop a dense assembly of hadrons from dissolving into a plasma of quarks and gluons. This new state of matter could be heated to a very high temperature and no limit was in sight. What is the meaning of Hagedorn temperature in this enlarged context?
In the SBM as conceived before quarks, hadrons were point particles. Now a subtle modification is required when considering quarks as building blocks. Hadrons made of quarks need a finite proper volume growing with hadron mass. Hagedorn and Rafelski discovered that at the Hagedorn temperature finite size hadrons dissolve into a quark-gluon liquid. Both a phase transition and a smoother transformation is possible, depending on the precise nature of the mass spectrum. The most physically attractive alternative was a first order phase transition. In this case the latent heat is delivered to the hadron phase at a constant Hagedorn temperature. One then reaches a new phase wherein the hadron constituents, the quarks and the gluons, are no longer confined. The system temperature can now rise again.
Phase Boundary of Matter
Within the study of hot hadronic matter the Hagedorn temperature is today understood as the phase boundary temperature between the hadron gas phase and the deconfined state of mobile quarks and gluons. Numerous experiments involving high energy nuclear collisions are underway at CERN-SPS and at the RHIC collider at Brookhaven National Laboratory (BNL) testing these new concepts. Nuclei, rather than protons, are used in these experiments in order to maximize the volume of quark deconfinement. This allows a more clear study of the signature of the formation of a new phase of matter, the quark-gluon plasmaQuark-gluon plasma
A quark–gluon plasma or quark soup is a phase of quantum chromodynamics which exists at extremely high temperature and/or density. This phase consists of asymptotically free quarks and gluons, which are several of the basic building blocks of matter...
(QGP).
Other Physics Areas
The concept of exponential growth in the number of states was originally proposed in the context of condensed matter physicsCondensed matter physics
Condensed matter physics deals with the physical properties of condensed phases of matter. These properties appear when a number of atoms at the supramolecular and macromolecular scale interact strongly and adhere to each other or are otherwise highly concentrated in a system. The most familiar...
. It was incorporated into high-energy physics in mid 1960. In hadronic physics, the Hagedorn temperature is today understood to be the deconfinement temperature of quarks, while in string theory, it indicates another phase transition: the transition at which very long strings are copiously produced. It is controlled by the size of the string tension which is smaller than the Planck scale by the some power of the coupling constant. By adjusting the tension to be small compared to the Planck scale, the Hagedorn transition can be much less than the Planck temperature
Planck temperature
Planck temperature is the greatest physically-possible temperature, according the set of theories proposed by the German physicist Max Planck. It's part of a system of five natural units known as Planck units, based on universal physical constants....
. Traditional grand-unified string models place this in the magnitude of 1030 kelvin
Kelvin
The kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
, two orders of magnitude smaller than the Planck temperature.

