
Gy's sampling theory
Encyclopedia
Gy's sampling theory is a theory
about the sampling of materials, developed by Pierre Gy
from the 1950s to beginning 2000s
in articles and books including:
The abbreviation TOS
is also used to denote Gy's sampling theory.
Gy's sampling theory uses a model in which the sample taking is represented by independent
Bernoulli trials for every particle in the parent population from which the sample is drawn. The two possible outcomes of each Bernoulli trial are: (1) the particle is selected and (2) the particle is not selected. The probability of selecting a particle may be different during each Bernoulli trial. The model used by Gy is mathematically equivalent to Poisson sampling
. Using this model, the following equation for the variance
of the sampling error
in the mass concentration in a sample was derived by Gy:
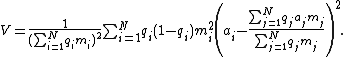
in which V is the variance of the sampling error, N is the number of particles in the population (before the sample was taken), q i is the probability of including the ith particle of the population in the sample (i.e. the first-order inclusion probability of the ith particle), m i is the mass of the ith particle of the population and a i is the mass concentration of the property of interest in the ith particle of the population.
It is noted that the above equation for the variance of the sampling error is an approximation based on a linearization
of the mass concentration in a sample.
In the theory of Gy, correct sampling
is defined as a sampling scenario in which all particles have the same probability of being included in the sample. This implies that q i no longer depends on i, and can therefore be replaced by the symbol q. Gy's equation for the variance of the sampling error becomes:
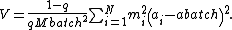
where abatch is the concentration of the property of interest in the population from which the sample is to be drawn and Mbatch is the mass of the population from which the sample is to be drawn. It has been noted that a similar equation had already been derived in 1935 by Kassel and Guy
.
Scientific theory
A scientific theory comprises a collection of concepts, including abstractions of observable phenomena expressed as quantifiable properties, together with rules that express relationships between observations of such concepts...
about the sampling of materials, developed by Pierre Gy
Pierre Gy
Pierre Maurice Gy is a chemist and statistician. Born in Paris, France, to Felix and Clemence, Gy graduated in chemical engineering from ESPCI ParisTech in 1946....
from the 1950s to beginning 2000s
in articles and books including:
- (1960) Sampling nomogram
- (1979) Sampling of particulate materials; theory and practice
- (1982) Sampling of particulate materials; theory and practice; 2nd edition
- (1992) Sampling of Heterogeneous and Dynamic Material Systems: Theories of Heterogeneity, Sampling and Homogenizing
- (1998) Sampling for Analytical Purposes
The abbreviation TOS
TOS
- General :* Terms of service, rules by which one must agree to abide by in order to use a service. Unless in violation of consumer protection laws, such terms are usually legally binding- Computing :...
is also used to denote Gy's sampling theory.
Gy's sampling theory uses a model in which the sample taking is represented by independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
Bernoulli trials for every particle in the parent population from which the sample is drawn. The two possible outcomes of each Bernoulli trial are: (1) the particle is selected and (2) the particle is not selected. The probability of selecting a particle may be different during each Bernoulli trial. The model used by Gy is mathematically equivalent to Poisson sampling
Poisson sampling
In the theory of finite population sampling, Poisson sampling is a sampling process where each element of the population that is sampled is subjected to an independent Bernoulli trial which determines whether the element becomes part of the sample during the drawing of a single sample.Each element...
. Using this model, the following equation for the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the sampling error
Sampling error
-Random sampling:In statistics, sampling error or estimation error is the error caused by observing a sample instead of the whole population. The sampling error can be found by subtracting the value of a parameter from the value of a statistic...
in the mass concentration in a sample was derived by Gy:
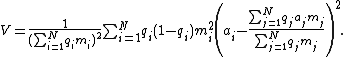
in which V is the variance of the sampling error, N is the number of particles in the population (before the sample was taken), q i is the probability of including the ith particle of the population in the sample (i.e. the first-order inclusion probability of the ith particle), m i is the mass of the ith particle of the population and a i is the mass concentration of the property of interest in the ith particle of the population.
It is noted that the above equation for the variance of the sampling error is an approximation based on a linearization
Linearization
In mathematics and its applications, linearization refers to finding the linear approximation to a function at a given point. In the study of dynamical systems, linearization is a method for assessing the local stability of an equilibrium point of a system of nonlinear differential equations or...
of the mass concentration in a sample.
In the theory of Gy, correct sampling
Correct sampling
During sampling of particulate materials, correct sampling is defined in Gy's sampling theory as a sampling scenario in which all particles in a population have the same probability of ending up in the sample ....
is defined as a sampling scenario in which all particles have the same probability of being included in the sample. This implies that q i no longer depends on i, and can therefore be replaced by the symbol q. Gy's equation for the variance of the sampling error becomes:
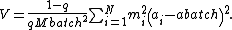
where abatch is the concentration of the property of interest in the population from which the sample is to be drawn and Mbatch is the mass of the population from which the sample is to be drawn. It has been noted that a similar equation had already been derived in 1935 by Kassel and Guy
.

