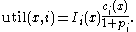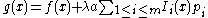Guided Local Search
Encyclopedia
Guided Local Search is a metaheuristic
search method. A meta-heuristic method is a method that sits on top of a local search algorithm
to change its behaviour.
Guided Local Search builds up penalties during a search. It uses penalties to help local search algorithms escape from local minima and plateaus. When the given local search algorithm settles in a local optimum, GLS modifies the objective function using a specific scheme (explained below). Then the local search will operate using an augmented objective function, which is designed to bring the search out of the local optimum. The key is in the way that the objective function is modified.
a cost function 
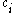is defined.
Each feature is also associated with a penalty
(initially set to 0) to record the number of occurrences of the feature in local minima.
The features and costs often come directly from the objective function. For example, in the traveling salesman problem, “whether the tour goes directly from city X to city Y” can be defined to be a feature. The distance between X and Y can be defined to be the cost. In the SAT and weighted MAX-SAT problems, the features can be “whether clause C satisfied by the current assignments”.
At the implementation level, we define for each feature
an Indicator Function 
indicating whether the feature is present in the current solution or not. 
is 1 when solution 
exhibits property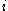 
, 0 otherwise.
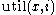, as defined below.
The idea is to penalise features that have high costs, although the utility of doing so decreases as the feature is penalised more and more often.
The parameter λ may be used to alter the intensification of the search for solutions. A higher value for λ will result in a more diverse search, where plateaus and basins are searched more coarsely; a low value will result in a more intensive search for the solution, where the plateaus and basins in the search landscape are searched in finer detail. The coefficient
is used to make the penalty part of the objective function balanced relative to changes in the objective function and is problem specific. A simple heuristic for setting 
is simply to record the average change in objective function up until the first local minimum, and then set 
to this value divided by the number of GLS features in the problem instance.
. A general version of the GLS algorithm, using a min-conflicts based hill climber (Minton et al. 1992) and based partly on GENET for constraint satisfaction and optimisation, has also been implemented in the Computer Aided Constraint Programming project.
The breakout method is very similar to GENET. It was designed for constraint satisfaction
.
Tabu search
is a class of search methods which can be instantiated to specific methods. GLS can be seen as a special case of Tabu search
.
By sitting GLS on top of genetic algorithm, Tung-leng Lau introduced the Guided Genetic Programming (GGA) algorithm. It was successfully applied to the general assignment problem (in scheduling), processors configuration problem (in electronic design) and a set of radio-link frequency assignment problems (an abstracted military application).
Choi et al. cast GENET as a Lagrangian search.
Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
search method. A meta-heuristic method is a method that sits on top of a local search algorithm
Local search (optimization)
In computer science, local search is a metaheuristic method for solving computationally hard optimization problems. Local search can be used on problems that can be formulated as finding a solution maximizing a criterion among a number of candidate solutions...
to change its behaviour.
Guided Local Search builds up penalties during a search. It uses penalties to help local search algorithms escape from local minima and plateaus. When the given local search algorithm settles in a local optimum, GLS modifies the objective function using a specific scheme (explained below). Then the local search will operate using an augmented objective function, which is designed to bring the search out of the local optimum. The key is in the way that the objective function is modified.
Solution features
To apply GLS, solution features must be defined for the given problem. Solution features are defined to distinguish between solutions with different characteristics, so that regions of similarity around local optima can be recognized and avoided. The choice of solution features depends on the type of problem, and also to a certain extent on the local search algorithm. 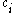For each feature a cost function is defined.Each feature is also associated with a penalty
(initially set to 0) to record the number of occurrences of the feature in local minima.The features and costs often come directly from the objective function. For example, in the traveling salesman problem, “whether the tour goes directly from city X to city Y” can be defined to be a feature. The distance between X and Y can be defined to be the cost. In the SAT and weighted MAX-SAT problems, the features can be “whether clause C satisfied by the current assignments”.
At the implementation level, we define for each feature
an Indicator Function indicating whether the feature is present in the current solution or not. is 1 when solution exhibits property 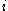, 0 otherwise.Selective penalty modifications
GLS computes the utility of penalising each feature. When the Local Search algorithm returns a local minimum x, GLS penalizes all those features (through increments to the penalty of the features) present in that solution which have maximum utility,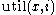, as defined below.
The idea is to penalise features that have high costs, although the utility of doing so decreases as the feature is penalised more and more often.
Searching through an augmented cost function
GLS uses an augmented cost function (defined below), to allow it to guide the Local Search algorithm out of the local minimum, through penalising features present in that local minimum. The idea is to make the local minimum more costly than the surrounding search space, where these features are not present.
The parameter λ may be used to alter the intensification of the search for solutions. A higher value for λ will result in a more diverse search, where plateaus and basins are searched more coarsely; a low value will result in a more intensive search for the solution, where the plateaus and basins in the search landscape are searched in finer detail. The coefficient
is used to make the penalty part of the objective function balanced relative to changes in the objective function and is problem specific. A simple heuristic for setting is simply to record the average change in objective function up until the first local minimum, and then set to this value divided by the number of GLS features in the problem instance.Extensions of Guided Local Search
Mills (2002) has described an Extended Guided Local Search (EGLS) which utilises random moves and an aspiration criterion designed specifically for penalty based schemes. The resulting algorithm improved the robustness of GLS over a range of parameter settings, particularly in the case of the quadratic assignment problemQuadratic assignment problem
The quadratic assignment problem is one of fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics, from the category of the facilities location problems....
. A general version of the GLS algorithm, using a min-conflicts based hill climber (Minton et al. 1992) and based partly on GENET for constraint satisfaction and optimisation, has also been implemented in the Computer Aided Constraint Programming project.
Related work
GLS was built on GENET, which was developed by Chang Wang, Edward Tsang and Andrew Davenport.The breakout method is very similar to GENET. It was designed for constraint satisfaction
Constraint satisfaction
In artificial intelligence and operations research, constraint satisfaction is the process of finding a solution to a set of constraints that impose conditions that the variables must satisfy. A solution is therefore a vector of variables that satisfies all constraints.The techniques used in...
.
Tabu search
Tabu search
Tabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
is a class of search methods which can be instantiated to specific methods. GLS can be seen as a special case of Tabu search
Tabu search
Tabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
.
By sitting GLS on top of genetic algorithm, Tung-leng Lau introduced the Guided Genetic Programming (GGA) algorithm. It was successfully applied to the general assignment problem (in scheduling), processors configuration problem (in electronic design) and a set of radio-link frequency assignment problems (an abstracted military application).
Choi et al. cast GENET as a Lagrangian search.