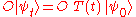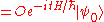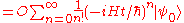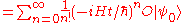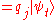Good quantum number
Encyclopedia
In quantum mechanics
, given a particular Hamiltonian
 and an operator
and an operator  with corresponding eigenvalues and eigenvectors given by
with corresponding eigenvalues and eigenvectors given by 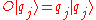 then the physical quantities
then the physical quantities 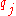 are said to be "good quantum numbers" if every eigenvector
are said to be "good quantum numbers" if every eigenvector 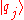 remains an eigenvector of
remains an eigenvector of  with the same eigenvalue as time evolves.
with the same eigenvalue as time evolves.
Hence, if:
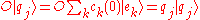
then we require
for all eigenvectors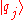 in order to call
in order to call 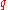 a good quantum number.
a good quantum number.
A necessary and sufficient condition for q to be good is that commute
commute
with the Hamiltonian . Proof:
. Proof:
Assume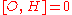 . If
. If 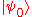 is an eigenvector of
is an eigenvector of  , then we have (by definition) that
, then we have (by definition) that 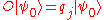 , and so :
, and so :
It can be said that a good classical analogue is that good quantum numbers are the equivalent of conserved quantities in classical mechanics, as their values do not change over time.In non-relativistic treatment,l and s are good quantum numbers but
in relativistic quantum mechanics they are no longer good quantum numbers as L and S do not commute with H(in Dirac theory). J=L+S is a good q.no. in relativistic quantum mechanics as J commutes with H.
Quantum mechanics
Quantum mechanics, also known as quantum physics or quantum theory, is a branch of physics providing a mathematical description of much of the dual particle-like and wave-like behavior and interactions of energy and matter. It departs from classical mechanics primarily at the atomic and subatomic...
, given a particular Hamiltonian
Hamiltonian (quantum mechanics)
In quantum mechanics, the Hamiltonian H, also Ȟ or Ĥ, is the operator corresponding to the total energy of the system. Its spectrum is the set of possible outcomes when one measures the total energy of a system...
 and an operator
and an operator  with corresponding eigenvalues and eigenvectors given by
with corresponding eigenvalues and eigenvectors given by 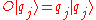 then the physical quantities
then the physical quantities 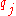 are said to be "good quantum numbers" if every eigenvector
are said to be "good quantum numbers" if every eigenvector 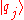 remains an eigenvector of
remains an eigenvector of  with the same eigenvalue as time evolves.
with the same eigenvalue as time evolves.Hence, if:
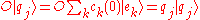
then we require
for all eigenvectors
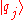 in order to call
in order to call 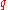 a good quantum number.
a good quantum number.A necessary and sufficient condition for q to be good is that
 commute
commuteCommutativity
In mathematics an operation is commutative if changing the order of the operands does not change the end result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it...
with the Hamiltonian
 . Proof:
. Proof:Assume
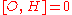 . If
. If 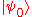 is an eigenvector of
is an eigenvector of  , then we have (by definition) that
, then we have (by definition) that 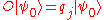 , and so :
, and so :It can be said that a good classical analogue is that good quantum numbers are the equivalent of conserved quantities in classical mechanics, as their values do not change over time.In non-relativistic treatment,l and s are good quantum numbers but
in relativistic quantum mechanics they are no longer good quantum numbers as L and S do not commute with H(in Dirac theory). J=L+S is a good q.no. in relativistic quantum mechanics as J commutes with H.