
Generalized linear array model
Encyclopedia
In statistics
, the generalized linear array model(GLAM) is used for analyzing data sets with array structures. It based on the generalized linear model
with the design matrix
written as a Kronecker product
.
s or GLMs whose model matrix can be written as a Kronecker product and whose data can be written as an array. In a large GLM, the GLAM approach gives very substantial savings in both storage and computational time over the usual GLM algorithm.
Suppose that the data is arranged in a
is arranged in a 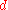 -dimensional array with size
-dimensional array with size  ; thus,the corresponding data vector
; thus,the corresponding data vector  has size
has size 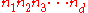 . Suppose also that the design matrix
. Suppose also that the design matrix
is of the form
The standard analysis of a GLM with data vector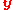 and design matrix
and design matrix  proceeds by repeated evaluation of the scoring algorithm
proceeds by repeated evaluation of the scoring algorithm
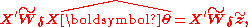
where represents the approximate solution of
represents the approximate solution of 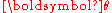 , and
, and  is the improved value of it;
is the improved value of it;  is the diagonal weight matrix with elements
is the diagonal weight matrix with elements
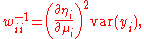
and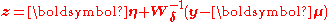
is the working variable.
Computationally, GLAM provides array algorithms to calculate the linear predictor,
and the weighted inner product
without evaluation of the model matrix
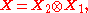 then the linear predictor is written
then the linear predictor is written  where
where 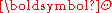 is the matrix of coefficients; the weighted inner product is obtained from
is the matrix of coefficients; the weighted inner product is obtained from  and
and  is the matrix of weights; here
is the matrix of weights; here 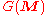 is the row tensor function of the
is the row tensor function of the 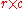 matrix
matrix  given by
given by
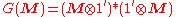
where means element by element multiplcation and
means element by element multiplcation and 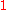 is a vector of 1's of length
is a vector of 1's of length  .
.
These low storage high speed formulae extend to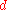 -dimensions.
-dimensions.
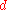 -dimensional smoothing problems where the data are arranged in an array and the smoothing matrix is constructed as a Kronecker product of
-dimensional smoothing problems where the data are arranged in an array and the smoothing matrix is constructed as a Kronecker product of 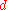 one-dimensional smoothing matrices.
one-dimensional smoothing matrices.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the generalized linear array model(GLAM) is used for analyzing data sets with array structures. It based on the generalized linear model
Generalized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
with the design matrix
Design matrix
In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
written as a Kronecker product
Kronecker product
In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix...
.
Overview
The generalized linear array model or GLAM was introduced in 2006. Such models provide a structure and a computational procedure for fitting generalized linear modelGeneralized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
s or GLMs whose model matrix can be written as a Kronecker product and whose data can be written as an array. In a large GLM, the GLAM approach gives very substantial savings in both storage and computational time over the usual GLM algorithm.
Suppose that the data
 is arranged in a
is arranged in a 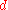 -dimensional array with size
-dimensional array with size  ; thus,the corresponding data vector
; thus,the corresponding data vector  has size
has size 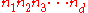 . Suppose also that the design matrix
. Suppose also that the design matrixDesign matrix
In statistics, a design matrix is a matrix of explanatory variables, often denoted by X, that is used in certain statistical models, e.g., the general linear model....
is of the form

The standard analysis of a GLM with data vector
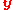 and design matrix
and design matrix  proceeds by repeated evaluation of the scoring algorithm
proceeds by repeated evaluation of the scoring algorithm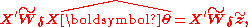
where
 represents the approximate solution of
represents the approximate solution of 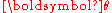 , and
, and  is the improved value of it;
is the improved value of it;  is the diagonal weight matrix with elements
is the diagonal weight matrix with elements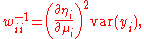
and
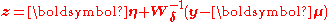
is the working variable.
Computationally, GLAM provides array algorithms to calculate the linear predictor,

and the weighted inner product

without evaluation of the model matrix

Example
In 2 dimensions, let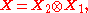 then the linear predictor is written
then the linear predictor is written  where
where 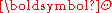 is the matrix of coefficients; the weighted inner product is obtained from
is the matrix of coefficients; the weighted inner product is obtained from  and
and  is the matrix of weights; here
is the matrix of weights; here 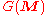 is the row tensor function of the
is the row tensor function of the 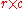 matrix
matrix  given by
given by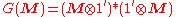
where
 means element by element multiplcation and
means element by element multiplcation and 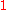 is a vector of 1's of length
is a vector of 1's of length  .
.These low storage high speed formulae extend to
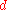 -dimensions.
-dimensions.Applications
GLAM is designed to be used in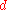 -dimensional smoothing problems where the data are arranged in an array and the smoothing matrix is constructed as a Kronecker product of
-dimensional smoothing problems where the data are arranged in an array and the smoothing matrix is constructed as a Kronecker product of 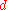 one-dimensional smoothing matrices.
one-dimensional smoothing matrices.

