Generalized assignment problem
Encyclopedia
In applied mathematics
, the maximum generalized assignment problem is a problem in combinatorial optimization
. This problem is a generalization
of the assignment problem
in which both tasks and agents have a size. Moreover, the size of each task might vary from one agent to the other.
This problem in its most general form is as follows:
There are a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost and profit that may vary depending on the agent-task assignment. Moreover, each agent has a budget and the sum of the costs of tasks assigned to it cannot exceed this budget. It is required to find an assignment in which all agents do not exceed their budget and total profit of the assignment is maximized.
.
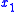through 
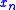and m kinds of bins 
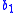through 
. Each bin 
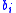is associated with a budget 
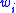. For a bin 
, each item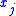 
has a profit 
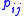and a weight 
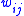. A solution is subset of items U and an assignment from U to the bins. A feasible solution is a solution in which for each bin 
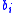the weights sum of assigned items is at most 
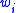. The solution's profit is the sum of profits for each item-bin assignment. The goal is to find a maximum profit feasible solution.
Mathematically the generalized assignment problem can be formulated as:
The generalized assignment problem is NP-hard
, and it is even APX-hard to approximate it. Recently it was shown that an extension of it is (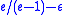
) hard to approximate for every 
.
-approximation algorithm for the knapsack problem, it is possible to construct a (
)-approximation for the generalized assignment problem in a greedy manner using a residual profit concept.
The algorithm constructs a schedule in iterations, where during iteration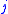
a tentative selection of items to bin 
is selected.
The selection for bin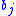
might change as items might be reselected in a later iteration for other bins.
The residual profit of an item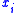
for bin 
is 
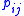if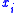 
is not selected for any other bin or 
– 
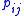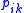if 
is selected for bin 
.
Formally: We use a vector
to indicate the tentative schedule during the algorithm. Specifically, 
means the item 
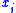is scheduled on bin 
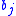and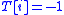 
means that item 
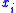is not scheduled. The residual profit in iteration 
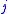is denoted by 
, where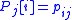 
if item 
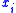is not scheduled (i.e. 
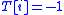) and 
if item 
is scheduled on bin 
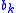(i.e.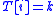 
).
Formally:
Applied mathematics
Applied mathematics is a branch of mathematics that concerns itself with mathematical methods that are typically used in science, engineering, business, and industry. Thus, "applied mathematics" is a mathematical science with specialized knowledge...
, the maximum generalized assignment problem is a problem in combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
. This problem is a generalization
Generalization
A generalization of a concept is an extension of the concept to less-specific criteria. It is a foundational element of logic and human reasoning. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteristics shared by those elements. As such, it...
of the assignment problem
Assignment problem
The assignment problem is one of the fundamental combinatorial optimization problems in the branch of optimization or operations research in mathematics...
in which both tasks and agents have a size. Moreover, the size of each task might vary from one agent to the other.
This problem in its most general form is as follows:
There are a number of agents and a number of tasks. Any agent can be assigned to perform any task, incurring some cost and profit that may vary depending on the agent-task assignment. Moreover, each agent has a budget and the sum of the costs of tasks assigned to it cannot exceed this budget. It is required to find an assignment in which all agents do not exceed their budget and total profit of the assignment is maximized.
Special cases
In the special case in which all the agents' budgets and all tasks' costs are equal to 1, this problem reduces to the maximum assignment problem. When the costs and profits of all agents-task assignment are equal, this problem reduces to the multiple knapsack problem. If there is a single agent, then, this problem reduces to the Knapsack problemKnapsack problem
The knapsack problem or rucksack problem is a problem in combinatorial optimization: Given a set of items, each with a weight and a value, determine the count of each item to include in a collection so that the total weight is less than or equal to a given limit and the total value is as large as...
.
Definition
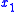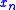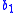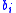In the following, we have n kinds of items, through and m kinds of bins through . Each bin is associated with a budget 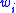. For a bin , each item 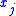has a profit 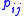and a weight 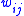. A solution is subset of items U and an assignment from U to the bins. A feasible solution is a solution in which for each bin 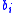the weights sum of assigned items is at most 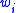. The solution's profit is the sum of profits for each item-bin assignment. The goal is to find a maximum profit feasible solution.Mathematically the generalized assignment problem can be formulated as:
- maximize
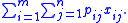
- subject to
;
;
;
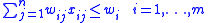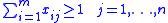The generalized assignment problem is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
, and it is even APX-hard to approximate it. Recently it was shown that an extension of it is (
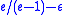) hard to approximate for every .Greedy approximation algorithm
Using any algorithm ALG-approximation algorithm for the knapsack problem, it is possible to construct a ()-approximation for the generalized assignment problem in a greedy manner using a residual profit concept.The algorithm constructs a schedule in iterations, where during iteration
a tentative selection of items to bin is selected.The selection for bin
might change as items might be reselected in a later iteration for other bins.The residual profit of an item
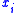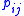for bin is if 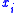is not selected for any other bin or 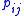– 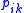if is selected for bin .Formally: We use a vector
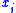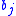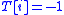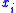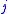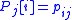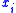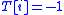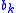to indicate the tentative schedule during the algorithm. Specifically, means the item is scheduled on bin and means that item is not scheduled. The residual profit in iteration is denoted by , where if item is not scheduled (i.e. ) and if item is scheduled on bin (i.e. 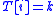).Formally:
- Set
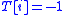for all 
- For
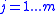do:
- Call ALG to find a solution to bin
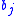using the residual profit function 
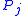. Denote the selected items by 
. - Update
using 
, i.e.,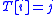 
for all 
.
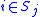- Call ALG to find a solution to bin