
Generalized Wiener process
Encyclopedia
In statistics
, a generalized Wiener process (named after Norbert Wiener
) is a continuous time random walk with drift and random jumps at every point in time. Formally:
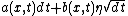
where a and b are deterministic functions, t is a continuous
index for time, x is a set of exogenous
variables that may change with time, dt is a differential
in time, and η is a random draw from a standard normal distribution at each instant.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a generalized Wiener process (named after Norbert Wiener
Norbert Wiener
Norbert Wiener was an American mathematician.A famous child prodigy, Wiener later became an early researcher in stochastic and noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.Wiener is regarded as the originator of cybernetics, a...
) is a continuous time random walk with drift and random jumps at every point in time. Formally:
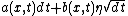
where a and b are deterministic functions, t is a continuous
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
index for time, x is a set of exogenous
Exogenous
Exogenous refers to an action or object coming from outside a system. It is the opposite of endogenous, something generated from within the system....
variables that may change with time, dt is a differential
Differential of a function
In calculus, the differential represents the principal part of the change in a function y = ƒ with respect to changes in the independent variable. The differential dy is defined bydy = f'\,dx,...
in time, and η is a random draw from a standard normal distribution at each instant.

