
Generalised hyperbolic distribution
Encyclopedia
The generalised hyperbolic distribution (GH) is a continuous probability distribution defined as the normal variance-mean mixture where the mixing distribution is the generalized inverse Gaussian distribution. Its probability density function
(see the box) is given in terms of modified Bessel function of the second kind, denoted by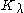 .
.
As the name suggests it is of a very general form, being the superclass of, among others, the Student's t-distribution, the Laplace distribution, the hyperbolic distribution
, the normal-inverse Gaussian distribution and the variance-gamma distribution.
It is mainly applied to areas that require sufficient probability of far-field behaviour, which it can model due to its semi-heavy tails—a property the normal distribution does not possess. The generalised hyperbolic distribution is often used in economics, with particular application in the fields of modelling financial markets and risk management, due to its semi-heavy tails. This class is closed under linear operations. It was introduced by Ole Barndorff-Nielsen.
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
(see the box) is given in terms of modified Bessel function of the second kind, denoted by
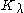 .
.As the name suggests it is of a very general form, being the superclass of, among others, the Student's t-distribution, the Laplace distribution, the hyperbolic distribution
Hyperbolic distribution
The hyperbolic distribution is a continuous probability distribution that is characterized by the fact that the logarithm of the probability density function is a hyperbola. Thus the distribution decreases exponentially, which is more slowly than the normal distribution...
, the normal-inverse Gaussian distribution and the variance-gamma distribution.
It is mainly applied to areas that require sufficient probability of far-field behaviour, which it can model due to its semi-heavy tails—a property the normal distribution does not possess. The generalised hyperbolic distribution is often used in economics, with particular application in the fields of modelling financial markets and risk management, due to its semi-heavy tails. This class is closed under linear operations. It was introduced by Ole Barndorff-Nielsen.
Related distributions
-
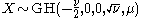 has a Student's t-distribution with
has a Student's t-distribution with  degrees of freedom.
degrees of freedom. -
 has a hyperbolic distributionHyperbolic distributionThe hyperbolic distribution is a continuous probability distribution that is characterized by the fact that the logarithm of the probability density function is a hyperbola. Thus the distribution decreases exponentially, which is more slowly than the normal distribution...
has a hyperbolic distributionHyperbolic distributionThe hyperbolic distribution is a continuous probability distribution that is characterized by the fact that the logarithm of the probability density function is a hyperbola. Thus the distribution decreases exponentially, which is more slowly than the normal distribution...
.
-
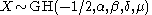 has a normal-inverse Gaussian distribution (NIG).
has a normal-inverse Gaussian distribution (NIG). -
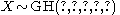 normal-inverse chi-squared distribution
normal-inverse chi-squared distribution -
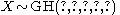 normal-inverse gamma distribution (NI)
normal-inverse gamma distribution (NI)
-
 has a variance-gamma distribution.
has a variance-gamma distribution.

