
Gauss-Bonnet gravity
Encyclopedia
In general relativity
, Einstein-Gauss-Bonnet gravity is a modification of the Einstein-Hilbert action
to include the Gauss-Bonnet term
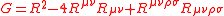
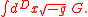
This term is only nontrivial in 4+1D or greater, and as such, only applies to extra dimensional models. In 3+1D and lower, it reduces to a topological surface term
. Despite being quadratic in the Riemann tensor (and Ricci tensor), terms containing more than 2 partial derivatives of the metric
cancel out, making the Euler-Lagrange equations second order quasilinear
partial differential equations in the metric. Consequently, there are no additional dynamical degrees of freedom, as in say f(R) gravity
.
More generally, we may consider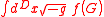
term for some function f. Nonlinearities in f render this coupling nontrivial even in 3+1D. However, fourth order terms reappear with the nonlinearities.
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, Einstein-Gauss-Bonnet gravity is a modification of the Einstein-Hilbert action
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
to include the Gauss-Bonnet term
Generalized Gauss-Bonnet theorem
In mathematics, the generalized Gauss–Bonnet theorem presents the Euler characteristic of a closed even-dimensional Riemannian manifold as an integral of a certain polynomial derived from its curvature...
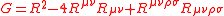
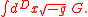
This term is only nontrivial in 4+1D or greater, and as such, only applies to extra dimensional models. In 3+1D and lower, it reduces to a topological surface term
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
. Despite being quadratic in the Riemann tensor (and Ricci tensor), terms containing more than 2 partial derivatives of the metric
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
cancel out, making the Euler-Lagrange equations second order quasilinear
Quasilinear
Quasilinear may refer to:* Quasilinear function, a function that is both quasiconvex and quasiconcave* Quasilinear utility, an economic utility function linear in one argument...
partial differential equations in the metric. Consequently, there are no additional dynamical degrees of freedom, as in say f(R) gravity
F(R) gravity
f gravity is a type of modified gravity theory first proposed in 1970by Buchdahl as a generalisation of Einstein's General Relativity. Although it is an active field of research, there are known problems with the theory...
.
More generally, we may consider
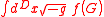
term for some function f. Nonlinearities in f render this coupling nontrivial even in 3+1D. However, fourth order terms reappear with the nonlinearities.

