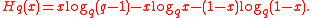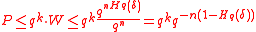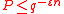GV-linear-code
Encyclopedia
In coding theory
, the bound of parameters such as rate R, relative distance, block length, etc. is usually concerned. Here Gilbert–Varshamov bound theorem claims the lower bound of the rate of the general code. More interestingly, Gilbert–Varshamov bound is the best in term of relative distance for codes over alphabets of size less than 49.
 . For every
. For every 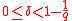 , and
, and  , there exists a code with rate
, there exists a code with rate 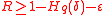 , and relative distance
, and relative distance  .
.
Here is the q-ary entropy function defined as follows:
is the q-ary entropy function defined as follows:
The above result was proved by Edgar Gilbert
for general code using the greedy method as here. For linear code
, Varshamov proved using the probabilistic method
for the random linear code. This proof will be shown in the following part.
High-level proof:
To show the existence of the linear code that satisfies those constraints, the probabilistic method
is used to construct the random linear code. Specifically the linear code is chosen randomly by choosing the random generator matrix in which the element is chosen uniformly over the field
in which the element is chosen uniformly over the field 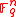 . Also the Hamming distance
. Also the Hamming distance
of the linear code is equal to the minimum weight of the codeword. So to prove that the linear code generated by has Hamming distance
has Hamming distance  , we will show that for any
, we will show that for any  . To prove that, we prove the opposite one; that is, the probability that the linear code generated by
. To prove that, we prove the opposite one; that is, the probability that the linear code generated by  has the Hamming distance less than
has the Hamming distance less than  is exponentially small in
is exponentially small in  . Then by probabilistic method, there exists the linear code satisfying the theorem.
. Then by probabilistic method, there exists the linear code satisfying the theorem.
Formal proof:
By using the probabilistic method, to show that there exists a linear code that has a Hamming distance greater than , we will show that the probability
, we will show that the probability
that the random linear code having the distance less than is exponentially small in
is exponentially small in  .
.
We know that the linear code is defined using the generator matrix
. So we use the "random generator matrix" as a mean to describe the randomness of the linear code. So a random generator matrix
as a mean to describe the randomness of the linear code. So a random generator matrix  of size
of size  contains
contains 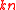 elements which are chosen independently and uniformly over the field
elements which are chosen independently and uniformly over the field 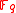 .
.
Recall that in a linear code, the distance = the minimum weight of the non-zero codeword. This fact is one of the properties of linear code
.
Denote be the weight of the codeword
be the weight of the codeword 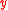 .
.
So
Coding theory
Coding theory is the study of the properties of codes and their fitness for a specific application. Codes are used for data compression, cryptography, error-correction and more recently also for network coding...
, the bound of parameters such as rate R, relative distance, block length, etc. is usually concerned. Here Gilbert–Varshamov bound theorem claims the lower bound of the rate of the general code. More interestingly, Gilbert–Varshamov bound is the best in term of relative distance for codes over alphabets of size less than 49.
Gilbert–Varshamov bound theorem
Theorem: Let . For every
. For every 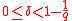 , and
, and  , there exists a code with rate
, there exists a code with rate 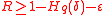 , and relative distance
, and relative distance  .
.Here
 is the q-ary entropy function defined as follows:
is the q-ary entropy function defined as follows:The above result was proved by Edgar Gilbert
Edgar Gilbert
Edgar Nelson Gilbert was an American mathematician and coding theorist, a longtime researcher at Bell Laboratories whose accomplishments include the Gilbert–Varshamov bound in coding theory, the Gilbert–Elliott model of bursty errors in signal transmission, and the Erdős–Rényi model for random...
for general code using the greedy method as here. For linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
, Varshamov proved using the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
for the random linear code. This proof will be shown in the following part.
High-level proof:
To show the existence of the linear code that satisfies those constraints, the probabilistic method
Probabilistic method
The probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
is used to construct the random linear code. Specifically the linear code is chosen randomly by choosing the random generator matrix
 in which the element is chosen uniformly over the field
in which the element is chosen uniformly over the field 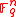 . Also the Hamming distance
. Also the Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
of the linear code is equal to the minimum weight of the codeword. So to prove that the linear code generated by
 has Hamming distance
has Hamming distance  , we will show that for any
, we will show that for any  . To prove that, we prove the opposite one; that is, the probability that the linear code generated by
. To prove that, we prove the opposite one; that is, the probability that the linear code generated by  has the Hamming distance less than
has the Hamming distance less than  is exponentially small in
is exponentially small in  . Then by probabilistic method, there exists the linear code satisfying the theorem.
. Then by probabilistic method, there exists the linear code satisfying the theorem.Formal proof:
By using the probabilistic method, to show that there exists a linear code that has a Hamming distance greater than
 , we will show that the probability
, we will show that the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
that the random linear code having the distance less than
 is exponentially small in
is exponentially small in  .
.We know that the linear code is defined using the generator matrix
Generator matrix
In coding theory, a generator matrix is a basis for a linear code, generating all its possible codewords.If the matrix is G and the linear code is C,where w is a codeword of the linear code C, c is a row vector, and a bijection exists between w and c. A generator matrix for an q-code has...
. So we use the "random generator matrix"
 as a mean to describe the randomness of the linear code. So a random generator matrix
as a mean to describe the randomness of the linear code. So a random generator matrix  of size
of size  contains
contains 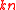 elements which are chosen independently and uniformly over the field
elements which are chosen independently and uniformly over the field 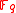 .
.Recall that in a linear code, the distance = the minimum weight of the non-zero codeword. This fact is one of the properties of linear code
Linear code
In coding theory, a linear code is an error-correcting code for which any linear combination of codewords is also a codeword. Linear codes are traditionally partitioned into block codes and convolutional codes, although Turbo codes can be seen as a hybrid of these two types. Linear codes allow for...
.
Denote
 be the weight of the codeword
be the weight of the codeword 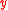 .
.So
-

Also if codeword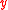 belongs to a linear code generated by
belongs to a linear code generated by  , then
, then  for some vector
for some vector  .
.
Therefore
By Boole's inequalityBoole's inequalityIn probability theory, Boole's inequality, also known as the union bound, says that for any finite or countable set of events, the probability that at least one of the events happens is no greater than the sum of the probabilities of the individual events...
, we have:
Now for a given message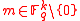 , we want to compute
, we want to compute 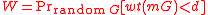
Denote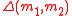 be a Hamming distance of two messages
be a Hamming distance of two messages  and
and 
Then for any message , we have:
, we have:  .
.
Using this fact, we can come up with the following equality:
Due to the randomness of ,
,  is a uniformly random vector from
is a uniformly random vector from  .
.
So
Let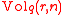 is a volume of Hamming ball with the radius
is a volume of Hamming ball with the radius  . Then:
. Then:
(The later inequality comes from the upper bound of the Volume of Hamming ball)
Then
By choosing , the above inequality becomes
, the above inequality becomes
Finally , which is exponentially small in n, that is what we want before. Then by the probabilistic method, there exists a linear code
, which is exponentially small in n, that is what we want before. Then by the probabilistic method, there exists a linear code  with relative distance
with relative distance 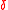 and rate
and rate  at least
at least 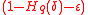 , which completes the proof.
, which completes the proof.
Comments
- The Varshamov construction above is not explicit; that is, it does not specify the deterministic method to construct the linear code that satisfies the Gilbert–Varshamov bound. The naive way that we can do is to go over all the generator matrices
 of size
of size 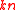 over the field
over the field  and check if that linear code has the satisfied Hamming distance. That leads to the exponential time algorithm to implement it.
and check if that linear code has the satisfied Hamming distance. That leads to the exponential time algorithm to implement it. - We also have a Las Vegas constructionLas Vegas algorithmIn computing, a Las Vegas algorithm is a randomized algorithm that always gives correct results; that is, it always produces the correct result or it informs about the failure. In other words, a Las Vegas algorithm does not gamble with the verity of the result; it gambles only with the resources...
that takes a random linear code and checks if this code has good Hamming distance. Nevertheless, this construction has the exponential running time.
See also
- Gilbert–Varshamov bound due to Gilbert construction for the general code
- Hamming BoundHamming boundIn mathematics and computer science, in the field of coding theory, the Hamming bound is a limit on the parameters of an arbitrary block code: it is also known as the sphere-packing bound or the volume bound from an interpretation in terms of packing balls in the Hamming metric into the space of...
- Probabilistic methodProbabilistic methodThe probabilistic method is a nonconstructive method, primarily used in combinatorics and pioneered by Paul Erdős, for proving the existence of a prescribed kind of mathematical object. It works by showing that if one randomly chooses objects from a specified class, the probability that the...
-