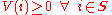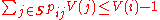Foster's theorem
Encyclopedia
In probability theory
, Foster's theorem, named after F. G. Foster, is used to draw conclusions about the positive recurrence of Markov chains with countable state spaces. It uses the fact that positive recurrent Markov chains exhibit a notion of "Lyapunov stability
" in terms of returning to any state while starting from it within a finite time interval.
Consider an aperiodic, irreducible discrete-time Markov chain on a countable state space
having a transition probability matrix 
. Foster's theorem states that the Markov chain is positive recurrent if and only if there exists a Lyapunov function
, such that
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, Foster's theorem, named after F. G. Foster, is used to draw conclusions about the positive recurrence of Markov chains with countable state spaces. It uses the fact that positive recurrent Markov chains exhibit a notion of "Lyapunov stability
Lyapunov stability
Various types of stability may be discussed for the solutions of differential equations describing dynamical systems. The most important type is that concerning the stability of solutions near to a point of equilibrium. This may be discussed by the theory of Lyapunov...
" in terms of returning to any state while starting from it within a finite time interval.
Consider an aperiodic, irreducible discrete-time Markov chain on a countable state space
having a transition probability matrix . Foster's theorem states that the Markov chain is positive recurrent if and only if there exists a Lyapunov functionLyapunov function
In the theory of ordinary differential equations , Lyapunov functions are scalar functions that may be used to prove the stability of an equilibrium of an ODE. Named after the Russian mathematician Aleksandr Mikhailovich Lyapunov, Lyapunov functions are important to stability theory and control...
, such that
